Question

10．已知△ABC中，AD为BC边上中线，若AB=6，AC=4，则AD的取值范围是1＜AD＜5．

Answer 1

分析 延长AD到E，使AD=DE，连接BE，证△ADC≌△EDB，推出AC=BE=4，在△ABE中，根据三角形三边关系定理得出AB-BE＜AE＜AB+BE，代入求出即可．

解答 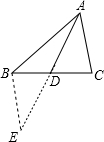解：延长AD到E，使AD=DE，连接BE，
∵AD是BC边上的中线，
∴BD=CD，
在△ADC和△EDB中，$\left\{\begin{array}{l}{AD=DE\\;}\\{∠ADC=∠EDB}\\{DC=BD\\;}\end{array}\right.$，
∴△ADC≌△EDB（SAS），
∴AC=BE=4，
在△ABE中，AB-BE＜AE＜AB+BE，
∴6-4＜2AD＜6+4，
∴1＜AD＜5，
故答案为：1＜AD＜5．

点评 本题考查了全等三角形的性质和判定，三角形的三边关系定理的应用，掌握本题的辅助线的作法是解题的关键．