题目内容
15. 阅读材料:
阅读材料:一般地,当α、β为任意角时,tan(α+β)与tan(α-β)的值可以用下面的公式求得:tan(α±β)=$\frac{tanα±tanβ}{1±tanα•tanβ}$.
例如:tan15°=tan(45°-30°)=$\frac{tan45°-tan30°}{1+tan45°•tan30°}$=$\frac{1-\frac{\sqrt{3}}{3}}{1+1×\frac{\sqrt{3}}{3}}$=$\frac{(3-\sqrt{3})}{(3+\sqrt{3})}$
=$\frac{(3-\sqrt{3})(3-\sqrt{3})}{(3+\sqrt{3})(3-\sqrt{3})}$=$\frac{12-6\sqrt{3}}{6}$=2-$\sqrt{3}$.
根据以上材料,解决下列问题:
(1)求tan75°的值;
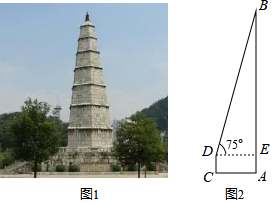
(2)都匀文峰塔,原名文笔塔,始建于明代万历年间,系五层木塔.文峰塔的木塔年久倾毁,仅存塔基.1983年,人民政府拨款维修文峰塔,成为今天的七层六面实心石塔(图1),小华想用所学知识来测量该铁塔的高度,如图2,已知小华站在离塔底中心A处5.7米的C处,测得塔顶的仰角为75°,小华的眼睛离地面的距离DC为1.72米,请帮助小华求出文峰塔AB的高度.(精确到1米,参考数据$\sqrt{3}$≈1.732,$\sqrt{2}$≈1.414)
分析 (1)利用题中的公式和特殊角的三角函数值计算75度的正切值;
(2)如图2,先在Rt△BDE中利用正切的定义计算出BE,然后计算BE+AE即可.
解答 解:(1)tan75°=tan(45°+30°)=$\frac{tan45°+tan30°}{1-tan45°•tan30°}$=$\frac{1+\frac{\sqrt{3}}{3}}{1-1×\frac{\sqrt{3}}{3}}$=$\frac{\sqrt{3}+1}{\sqrt{3}-1}$=2+$\sqrt{3}$;
(2)如图2,易得DE=CA=5.7,AE=CD=1.72,
在Rt△BDE中,∵tan∠BDE=$\frac{BE}{DE}$,
∴BE=DEtan75°=5.7×(2+$\sqrt{3}$)≈21.2724,
∴AB=BE+AE=21.2724+1.72≈23(m).
答:文峰塔AB的高度约为23m.
点评 本题考查了解直角三角形的应用-仰角俯角:解决此类问题要了解角之间的关系,找到与已知和未知相关联的直角三角形,当图形中没有直角三角形时,要通过作高或垂线构造直角三角形,另当问题以一个实际问题的形式给出时,要善于读懂题意,把实际问题划归为直角三角形中边角关系问题加以解决.

练习册系列答案
相关题目
4.下列各组数中,互为相反数的一组是( )
| A. | -(-8)与+(+8) | B. | -(+8)与-|-8| | C. | -|-8|与+(-8) | D. | -22与(-2)2 |
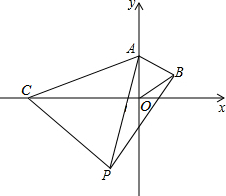 如图,在直角坐标系中,点A的坐标是(0,2),点C是x轴上的一个动点,点C在x轴上移动时,始终保持△ACP是等边三角形,当点C移动到点O时,得到等边三角形AOB(此时点P与点B重合).
如图,在直角坐标系中,点A的坐标是(0,2),点C是x轴上的一个动点,点C在x轴上移动时,始终保持△ACP是等边三角形,当点C移动到点O时,得到等边三角形AOB(此时点P与点B重合).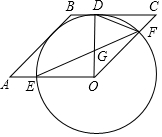 已知:四边形OABC是菱形,以O为圆心作⊙O,与BC相切于点D,交OA于E,交OC于F,连接OD,DF.
已知:四边形OABC是菱形,以O为圆心作⊙O,与BC相切于点D,交OA于E,交OC于F,连接OD,DF. (1)比较大小:$\sqrt{5}$+1>$\sqrt{10}$(填“>”、“<”或者“=”);
(1)比较大小:$\sqrt{5}$+1>$\sqrt{10}$(填“>”、“<”或者“=”); 阅读下面材料:
阅读下面材料: