题目内容
7. 阅读下面材料:
阅读下面材料:通过整式运算一章的学习,我们发现要验证一个结论的正确性可以有两种方法:
例如:要验证结论(a+b)2-(a-b)2=4ab
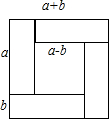
方法1:几何图形验证:如右图,我们可以将一个边长为(a+b)的正方形上裁去一个边长为(a-b)的小正方形则剩余图形的面积为4ab,验证该结论正确.
方法2:代数法验证:等式左边=
$\begin{array}{l}{(a+b)^2}-{(a-b)^2}\\={a^2}+2ab+{b^2}-({a^2}-2ab+{b^2})\\={a^2}+2ab+{b^2}-{a^2}+2ab-{b^2}\\=4ab\end{array}$
所以,左边=右边,结论成立.
观察下列各式:
22-12=2×1+1
32-22=2×2+1
42-32=2×3+1
…
(1)按规律,请写出第n个等式(n+1)2-n2=2n+1;
(2)试分别用两种方法验证这个结论的正确性.
分析 (1)根据题意给出规律即可求出答案.
(2)根据题意给出的方法即可求出验证
解答 解:(1)(n+1)2-n2=2n+1 (2)方法一:几何图形验证:
(2)方法一:几何图形验证:
如右图,我们可以将一个边长为(n+1)的正方形上裁去一个边长为n的小正方形则剩余图形的面积为2n+1,
验证该结论正确.
方法二:左边=(n+1)2-n2
=n2+2n+1-n2
=2n+1=右边
所以,左边=右边,结论成立.
故答案为:(1)(n+1)2-n2=2n+1
点评 本题考查整式的运算,解题的关键是正确理解题意,本题属于基础题型.

练习册系列答案
相关题目
17.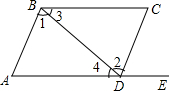 如图,给出下列条件:①∠1=∠2;②∠3=∠4;③∠A=∠CDE;④AD∥BC,且∠A=∠C.其中,能推出AB∥DC的条件为( )
如图,给出下列条件:①∠1=∠2;②∠3=∠4;③∠A=∠CDE;④AD∥BC,且∠A=∠C.其中,能推出AB∥DC的条件为( )
 如图,给出下列条件:①∠1=∠2;②∠3=∠4;③∠A=∠CDE;④AD∥BC,且∠A=∠C.其中,能推出AB∥DC的条件为( )
如图,给出下列条件:①∠1=∠2;②∠3=∠4;③∠A=∠CDE;④AD∥BC,且∠A=∠C.其中,能推出AB∥DC的条件为( )| A. | ①④ | B. | ②③ | C. | ①③ | D. | ①③④ |
12.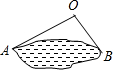 如图,为估计池塘岸边A,B的距离,小明在池塘的一侧选取一点O,测得OA=15米,OB=10米,A,B间的距离可能是( )
如图,为估计池塘岸边A,B的距离,小明在池塘的一侧选取一点O,测得OA=15米,OB=10米,A,B间的距离可能是( )
 如图,为估计池塘岸边A,B的距离,小明在池塘的一侧选取一点O,测得OA=15米,OB=10米,A,B间的距离可能是( )
如图,为估计池塘岸边A,B的距离,小明在池塘的一侧选取一点O,测得OA=15米,OB=10米,A,B间的距离可能是( )| A. | 30米 | B. | 25米 | C. | 20米 | D. | 5米 |
17. 某校学生准备调查七年级学生参加“A.武术类”、“B.书画类”、“C.棋牌类”、“D.器乐类”四类校本课程的人数.
某校学生准备调查七年级学生参加“A.武术类”、“B.书画类”、“C.棋牌类”、“D.器乐类”四类校本课程的人数.
(1)确定调查方式时,甲同学说:“我到七年级(1)班调查全体同学”;乙同学说:“放学时我到校门口随机调查部分同学”;丙同学说:“我到七年级每个班随机调查一定数量的同学”.请指出哪位同学的调查方式最合理.
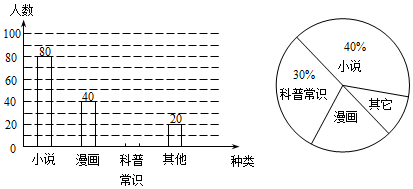
(2)他们采用了最为合理的调查方法收集数据,并绘制了如图所示的统计表和扇形统计图.
请你根据以上图表提供的信息解答下列问题:
①求a=100,b=0.15;
②在扇形统计图中,器乐类所对应扇形的圆心角的度数是144°;
③若该校七年级有学生560人,请你估计大约有多少学生参加武术类校本课程.
(3)甲、乙2人对这四类课程的喜爱撑多久基本相同,决定分别从中任意选择1类参加,求甲、乙2人选择同1类课程的概率.
 某校学生准备调查七年级学生参加“A.武术类”、“B.书画类”、“C.棋牌类”、“D.器乐类”四类校本课程的人数.
某校学生准备调查七年级学生参加“A.武术类”、“B.书画类”、“C.棋牌类”、“D.器乐类”四类校本课程的人数.(1)确定调查方式时,甲同学说:“我到七年级(1)班调查全体同学”;乙同学说:“放学时我到校门口随机调查部分同学”;丙同学说:“我到七年级每个班随机调查一定数量的同学”.请指出哪位同学的调查方式最合理.
(2)他们采用了最为合理的调查方法收集数据,并绘制了如图所示的统计表和扇形统计图.
| 类别 | 频数(人数) | 频率 |
| 武术类 | 0.25 | |
| 书画类 | 20 | 0.20 |
| 棋牌类 | 15 | b |
| 器乐类 | ||
| 合计 | a | 1.00 |
①求a=100,b=0.15;
②在扇形统计图中,器乐类所对应扇形的圆心角的度数是144°;
③若该校七年级有学生560人,请你估计大约有多少学生参加武术类校本课程.
(3)甲、乙2人对这四类课程的喜爱撑多久基本相同,决定分别从中任意选择1类参加,求甲、乙2人选择同1类课程的概率.
 如图,正方形ABCD的边长为1,点E在边AB上,连接ED,过点D作FD⊥DE与BC的延长线相交于点F,连接EF与边CD相交于点G、与对角线BD相交于点H.
如图,正方形ABCD的边长为1,点E在边AB上,连接ED,过点D作FD⊥DE与BC的延长线相交于点F,连接EF与边CD相交于点G、与对角线BD相交于点H. 阅读材料:
阅读材料: