题目内容
3.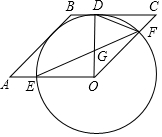 已知:四边形OABC是菱形,以O为圆心作⊙O,与BC相切于点D,交OA于E,交OC于F,连接OD,DF.
已知:四边形OABC是菱形,以O为圆心作⊙O,与BC相切于点D,交OA于E,交OC于F,连接OD,DF.(1)求证:AB是⊙O的切线;
(2)连接EF交OD于点G,若∠C=45°,求证:GF2=DG•OE.
分析 (1)过O作OH⊥AB,由菱形的性质可求得OH=OD,由切线的性质可知OD为圆O的半径,可得OH为圆O的半径,可证得结论;
(2)由条件可证明△DGF∽△DFO,再利用相似三角形的性质可证得结论.
解答 证明:
(1)如图,过O作OH⊥AB,
∵四边形OABC为菱形,
∴AB=BC,
∵BC为⊙O的切线,
∴OD⊥BC,且OD为⊙O的半径,
∴AB•OH=BC•OD,
∴OH=OD,
∴AB为⊙O的切线;
(2)由(1)可知OD⊥CB,
∴AO⊥DO,
∴∠AOD=90°,
∴∠DFO=$\frac{1}{2}$∠AOD=45°,
∵∠C=45°,且∠ODC=90°,
∴∠DOF=45°,
在△OGF中,∠DGF为△OGF的外角,
∴∠DGF=∠DOF+∠GFO=45°+∠GFO,
∵∠DFO=∠DFG+∠GFO=45°+∠GFO,
∴∠DGF=∠DFO,且∠GDF=∠FDO,
∴△DGF∽△DFO,
∴$\frac{DG}{DF}$=$\frac{GF}{OF}$,即DF•GF=DG•OF,
∵OF=OD=OE,
∴DF=GF,
∴GF2=DG•OE.
点评 本题主要考查切线的判定和性质及相似三角形的判定,掌握切线的判定方法和相似三角形的判定方法是解题的关键,注意等积法的应用.

练习册系列答案
 课堂全解字词句段篇章系列答案
课堂全解字词句段篇章系列答案 步步高口算题卡系列答案
步步高口算题卡系列答案 点睛新教材全能解读系列答案
点睛新教材全能解读系列答案
相关题目
13.在弹簧限度内,弹簧挂上物体后弹簧的长度与所挂物体的质量之间的关系如下表:
(1)上表中,自变量是物体的质量,因变量是弹簧的长度.
(2)弹簧不挂物体时的长度是12cm.
(3)如果用x表示弹性限度内物体的质量,用y表示弹簧的长度,那么随着x的变化,y的变化趋势是增长.
(4)写出y与x的关系式y=0.5x+12.
(5)如果弹簧最大挂重量为25千克,你能预测当挂重为14千克时,弹簧的长度是多少?
| 所挂物体的质量/千克 | 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 |
| 弹簧的长度/cm | 12 | 12.5 | 13 | 13.5 | 14 | 14.5 | 15 | 15.5 | 16 |
(2)弹簧不挂物体时的长度是12cm.
(3)如果用x表示弹性限度内物体的质量,用y表示弹簧的长度,那么随着x的变化,y的变化趋势是增长.
(4)写出y与x的关系式y=0.5x+12.
(5)如果弹簧最大挂重量为25千克,你能预测当挂重为14千克时,弹簧的长度是多少?
11.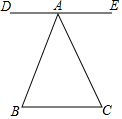 如图,ED∥BC,∠B=∠C,则下列正确的是( )
如图,ED∥BC,∠B=∠C,则下列正确的是( )
 如图,ED∥BC,∠B=∠C,则下列正确的是( )
如图,ED∥BC,∠B=∠C,则下列正确的是( )| A. | ∠BAE=∠DAC | B. | ∠BAE=∠ACB | C. | ∠ABC=∠DAC | D. | ∠BAC=∠DAC |
12.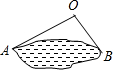 如图,为估计池塘岸边A,B的距离,小明在池塘的一侧选取一点O,测得OA=15米,OB=10米,A,B间的距离可能是( )
如图,为估计池塘岸边A,B的距离,小明在池塘的一侧选取一点O,测得OA=15米,OB=10米,A,B间的距离可能是( )
 如图,为估计池塘岸边A,B的距离,小明在池塘的一侧选取一点O,测得OA=15米,OB=10米,A,B间的距离可能是( )
如图,为估计池塘岸边A,B的距离,小明在池塘的一侧选取一点O,测得OA=15米,OB=10米,A,B间的距离可能是( )| A. | 30米 | B. | 25米 | C. | 20米 | D. | 5米 |
 如图,正方形ABCD的边长为1,点E在边AB上,连接ED,过点D作FD⊥DE与BC的延长线相交于点F,连接EF与边CD相交于点G、与对角线BD相交于点H.
如图,正方形ABCD的边长为1,点E在边AB上,连接ED,过点D作FD⊥DE与BC的延长线相交于点F,连接EF与边CD相交于点G、与对角线BD相交于点H. 阅读材料:
阅读材料: