题目内容
3.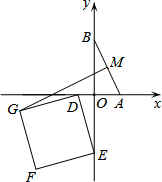 在平面直角坐标系xOy中,点A、B分别在x轴、y轴的正半轴上运动,点M为线段AB的中点.点D、E分别在x轴、y轴的负半轴上运动,且DE=AB=10.以DE为边在第三象限内作正方形DGFE,则线段MG长度的最大值为10+5$\sqrt{5}$.
在平面直角坐标系xOy中,点A、B分别在x轴、y轴的正半轴上运动,点M为线段AB的中点.点D、E分别在x轴、y轴的负半轴上运动,且DE=AB=10.以DE为边在第三象限内作正方形DGFE,则线段MG长度的最大值为10+5$\sqrt{5}$.
分析 取DE的中点N,连结ON、NG、OM.根据勾股定理可得NG=5$\sqrt{5}$.在点M与G之间总有MG≤MO+ON+NG(如图1),M、O、N、G四点共线,此时等号成立(如图2).可得线段MG取最大值10+5$\sqrt{5}$.
解答 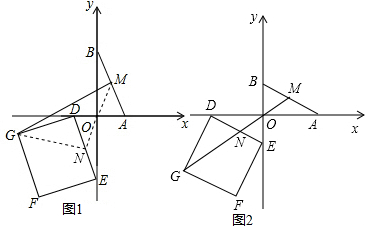 解:取DE的中点N,连结ON、NG、OM.
解:取DE的中点N,连结ON、NG、OM.
∵∠AOB=90°,
∴OM=$\frac{1}{2}$AB=5.
同理ON=5.
∵正方形DGFE,N为DE中点,DE=10,
∴NG=$\sqrt{D{N}^{2}+D{G}^{2}}$=$\sqrt{1{0}^{2}+{5}^{2}}$=5$\sqrt{5}$.
在点M与G之间总有MG≤MO+ON+NG(如图1),
由于∠DNG的大小为定值,只要∠DON=$\frac{1}{2}$∠DNG,且M、N关于点O中心对称时,M、O、N、G四点共线,此时等号成立(如图2).
∴线段MG取最大值10+5$\sqrt{5}$.
故答案为:10+5$\sqrt{5}$.
点评 此题考查了直角三角形的性质,勾股定理,四点共线的最值问题,得出M、O、N、G四点共线,则线段MG长度的最大是解题关键.

练习册系列答案
相关题目
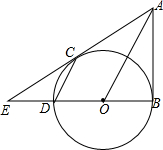 如图,过点A作⊙O的切线AB,AC,切点分别为B,C,直径BD的延长线与直线AC交于E,连接DC、OA.
如图,过点A作⊙O的切线AB,AC,切点分别为B,C,直径BD的延长线与直线AC交于E,连接DC、OA.
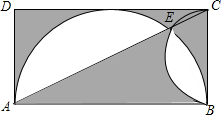 如图,长方形的长AB为8厘米,宽BC为4厘米,分别以AB、BC为直径画半圆,两个半圆的交点E在线段AC上,求阴影部分的面积.(π取3.14)
如图,长方形的长AB为8厘米,宽BC为4厘米,分别以AB、BC为直径画半圆,两个半圆的交点E在线段AC上,求阴影部分的面积.(π取3.14)