题目内容
4.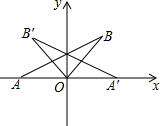 如图,在△AOB中,OA=OB,∠AOB=135°,点A的坐标为(-1,0),△AOB与△A′OB′关于y轴对称,则点B′的坐标为(-$\frac{\sqrt{2}}{2}$,$\frac{\sqrt{2}}{2}$).
如图,在△AOB中,OA=OB,∠AOB=135°,点A的坐标为(-1,0),△AOB与△A′OB′关于y轴对称,则点B′的坐标为(-$\frac{\sqrt{2}}{2}$,$\frac{\sqrt{2}}{2}$).
分析 根据等腰直角三角形的性质,可得B点坐标,根据关于y轴对称的点,纵坐标相同,横坐标互为相反数,可得答案.
解答 解:如图,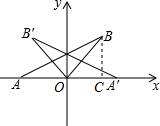 过点B作BC⊥x轴于点C,
过点B作BC⊥x轴于点C,
由△AOB中,OA=OB,∠AOB=135°,点A的坐标为(-1,0),
得∠BOA′=45,BC=BO•sin∠BOC=$\frac{\sqrt{2}}{2}$,OC=OB•cos∠BOC=$\frac{\sqrt{2}}{2}$,
即B($\frac{\sqrt{2}}{2}$,$\frac{\sqrt{2}}{2}$).
由B′与B关于y轴对称,得
B′(-$\frac{\sqrt{2}}{2}$,$\frac{\sqrt{2}}{2}$),
故答案为:(-$\frac{\sqrt{2}}{2}$,$\frac{\sqrt{2}}{2}$).
点评 本题考查了关于y轴对称的点的坐标,解决本题的关键是掌握好对称点的坐标规律:关于x轴对称的点,横坐标相同,纵坐标互为相反数;关于y轴对称的点,纵坐标相同,横坐标互为相反数;关于原点对称的点,横坐标与纵坐标都互为相反数.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
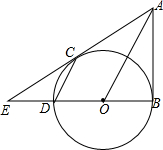 如图,过点A作⊙O的切线AB,AC,切点分别为B,C,直径BD的延长线与直线AC交于E,连接DC、OA.
如图,过点A作⊙O的切线AB,AC,切点分别为B,C,直径BD的延长线与直线AC交于E,连接DC、OA.