题目内容
某汽车租赁公司拥有20辆汽车.据统计,当每辆车的日租金为400元时,可全部租出;当每 辆车的日租金每增加50元,未租出的车将增加1辆;公司平均每日的各项支出共4800元.设公司每日租出x辆车时,日收益为y元.(日收益=日租金收入一平均每日各项支出)
(1)公司每日租出x辆车时,每辆车的日租金为多少元(用含x的代数式表示);
(2)当每日租出多少辆时,租赁公司日收益最大?最大是多少元?
(3)当每日租出多少辆时,租赁公司的日收益不盈也不亏?
(1)公司每日租出x辆车时,每辆车的日租金为多少元(用含x的代数式表示);
(2)当每日租出多少辆时,租赁公司日收益最大?最大是多少元?
(3)当每日租出多少辆时,租赁公司的日收益不盈也不亏?
考点:二次函数的应用,一元二次方程的应用
专题:
分析:(1)由租出x辆汽车,就有(20-x)辆没有租出,每辆车的租金就增加50(20-x)元,就可以求出每辆车的日租金;
(2)根据日收益=日租金收入一平均每日各项支出求出y与x之间的函数关系式,化为顶点式就可以求出结论;
(3)当y=0时建立一元二次方程求出其解即可.
(2)根据日收益=日租金收入一平均每日各项支出求出y与x之间的函数关系式,化为顶点式就可以求出结论;
(3)当y=0时建立一元二次方程求出其解即可.
解答:解:(1)由题意,得
400+50(20-x)=1400-50x.
答:每辆车的日租金为(1400-50x)元
(2)由题意,得
y=x(1400-50x)-4800=-50(x-14)2+5000
∴a=-50<0,
∴当x=14时,y最大=5000.
答:每日租出14辆时,租赁公司日收益最大,最大是5000元
(3)当y=0时,
0=-50(x-14)2+5000
解得:x1=24>20(舍去),x2=4,
答:当每日租出4辆时,租赁公司的日收益不盈也不亏.
400+50(20-x)=1400-50x.
答:每辆车的日租金为(1400-50x)元
(2)由题意,得
y=x(1400-50x)-4800=-50(x-14)2+5000
∴a=-50<0,
∴当x=14时,y最大=5000.
答:每日租出14辆时,租赁公司日收益最大,最大是5000元
(3)当y=0时,
0=-50(x-14)2+5000
解得:x1=24>20(舍去),x2=4,
答:当每日租出4辆时,租赁公司的日收益不盈也不亏.
点评:本题考查了代数式表示数的运用,二次函数的性质的运用,一元二次方程的解法的运用,日收益=日租金收入一平均每日各项支出的运用,解答时求出函数的解析式是关键.

练习册系列答案
相关题目
若关于x的方程
=
有增根,则m的值是( )
| x-1 |
| x-2 |
| m |
| x-2 |
| A、0 | B、l | C、2 | D、3 |
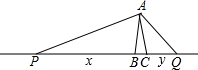 如图,在△ABC中,AB=AC=3,∠BAC=20°.动点P,Q分别在直线BC上运动,且始终保持∠PAQ=100°.设BP=x,CQ=y,则y与x之间的函数关系式为
如图,在△ABC中,AB=AC=3,∠BAC=20°.动点P,Q分别在直线BC上运动,且始终保持∠PAQ=100°.设BP=x,CQ=y,则y与x之间的函数关系式为 如图,梯形ABCD中.AB∥CD.且AB=2CD,E,F分别是AB,BC的中点.EF与BD相交于点M.
如图,梯形ABCD中.AB∥CD.且AB=2CD,E,F分别是AB,BC的中点.EF与BD相交于点M. ?已知C是
?已知C是