题目内容
 ?已知C是
?已知C是 |
| AB |
考点:垂径定理,勾股定理
专题:计算题
分析:由C是
的中点,根据平分弦所对一条弧的直径,垂直平分弦,并且平分弦所对的另一条弧得到OC⊥AB,弧AC=弧BD,则∠AOC=
∠AOB=60°,然后在Rt△AOD中利用含30度的直角三角形三边的关系求解.
 |
| AB |
| 1 |
| 2 |
解答:解:∵C是
的中点,
∴OC⊥AB,弧AC=弧BD,
∴∠AOC=∠BOC=
∠AOB=60°,
在Rt△AOD中,∵AD=8,∠AOD=60°,
∴∠A=30°,
∴OD=
AD=
,
∴OA=2OD=
.
 |
| AB |
∴OC⊥AB,弧AC=弧BD,
∴∠AOC=∠BOC=
| 1 |
| 2 |
在Rt△AOD中,∵AD=8,∠AOD=60°,
∴∠A=30°,
∴OD=
| ||
| 3 |
8
| ||
| 3 |
∴OA=2OD=
16
| ||
| 3 |
点评:本题考查了垂径定理的推论:平分弦(不是直径)的直径平分这条弦,并且平分弦所对的两条弧;平分弦所对一条弧的直径,垂直平分弦,并且平分弦所对的另一条弧.也考查了勾股定理.

练习册系列答案
相关题目
 如图,E是等边△ABC中AC边上的点,∠1=∠2,BE=CD,试判断△ADE的形状.
如图,E是等边△ABC中AC边上的点,∠1=∠2,BE=CD,试判断△ADE的形状.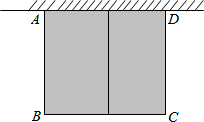 如图,有长为24米的篱笆,围成中间隔有一道篱笆的长方形的花圃,且花圃的长可借用一段墙体(墙体的最大可用长度a=10米).如果AB的长为x,面积为y,
如图,有长为24米的篱笆,围成中间隔有一道篱笆的长方形的花圃,且花圃的长可借用一段墙体(墙体的最大可用长度a=10米).如果AB的长为x,面积为y, 如图,△ABC和△A′B′C′关于直线m对称,∠C′=80°,∠A=50°,AB=a,B′C′=b,则∠C=
如图,△ABC和△A′B′C′关于直线m对称,∠C′=80°,∠A=50°,AB=a,B′C′=b,则∠C= 如图,将下列八根火柴拼成的两个菱形,移动两根火柴使其变成一个菱形.
如图,将下列八根火柴拼成的两个菱形,移动两根火柴使其变成一个菱形.