题目内容
 如图,梯形ABCD中.AB∥CD.且AB=2CD,E,F分别是AB,BC的中点.EF与BD相交于点M.
如图,梯形ABCD中.AB∥CD.且AB=2CD,E,F分别是AB,BC的中点.EF与BD相交于点M.(1)求证:△EDM∽△FBM;
(2)若EF=12,求EM.
考点:梯形,平行四边形的判定与性质,相似三角形的判定与性质
专题:
分析:(1)能够根据已知条件证明四边形BCDE是平行四边形,从而得到DE∥BC,即可证明相似;
(2)根据相似三角形的性质求得相似比,即可求得线段的长.
(2)根据相似三角形的性质求得相似比,即可求得线段的长.
解答:(1)证明:∵点E、F分别是AB、BC的中点且AB=2CD,
∴BE=CD.
∵AB∥CD,
∴四边形BEDC是平行四边形.
∴DE∥BF.
∴∠EDM=∠FBM.
∵∠DME=∠BMF,
∴△EDM∽△FBM.
(2)解:∵△EDM∽△FBM,
∴BF=
DE.
∵
=
,
∴DM=2BM.
∵BD=DM+BM=12,
∴BM=4.
∴BE=CD.
∵AB∥CD,
∴四边形BEDC是平行四边形.
∴DE∥BF.
∴∠EDM=∠FBM.
∵∠DME=∠BMF,
∴△EDM∽△FBM.
(2)解:∵△EDM∽△FBM,
∴BF=
| 1 |
| 2 |
∵
| DE |
| BF |
| DM |
| BM |
∴DM=2BM.
∵BD=DM+BM=12,
∴BM=4.
点评:此题考查了相似三角形的判定与性质,平行四边形的判定与性质,以及比例的性质,要证明比例问题常常把各边放入两三角形中,利用相似解决问题,证明相似的方法有:两对对应边相等的两三角形相似;两边对应成比例且夹角相等的两三角形相似;三边对应成比例的两三角形相似等,此外学生在做第二问时要注意借助已证的结论.

练习册系列答案
 轻巧夺冠周测月考直通中考系列答案
轻巧夺冠周测月考直通中考系列答案
相关题目
下列图形既是轴对称图形,又是中心对称图形的是( )
A、 |
B、 |
C、 |
D、 |
 抛物线与直线y=m的交点,图中抛物线的解析式为y=ax2+bx+c,根据图象判断下列方程根的情况.
抛物线与直线y=m的交点,图中抛物线的解析式为y=ax2+bx+c,根据图象判断下列方程根的情况.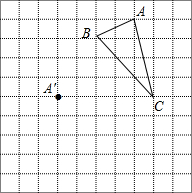 在正方形网格中,每个小正方形的边长均为1个单位长度,△ABC三个顶点的位置如图所示,现将△ABC平移,使点A移动到点A′,点B′、C′分别是B、C的对应点.
在正方形网格中,每个小正方形的边长均为1个单位长度,△ABC三个顶点的位置如图所示,现将△ABC平移,使点A移动到点A′,点B′、C′分别是B、C的对应点. 如图,E是等边△ABC中AC边上的点,∠1=∠2,BE=CD,试判断△ADE的形状.
如图,E是等边△ABC中AC边上的点,∠1=∠2,BE=CD,试判断△ADE的形状.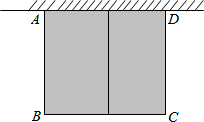 如图,有长为24米的篱笆,围成中间隔有一道篱笆的长方形的花圃,且花圃的长可借用一段墙体(墙体的最大可用长度a=10米).如果AB的长为x,面积为y,
如图,有长为24米的篱笆,围成中间隔有一道篱笆的长方形的花圃,且花圃的长可借用一段墙体(墙体的最大可用长度a=10米).如果AB的长为x,面积为y,