��Ŀ����
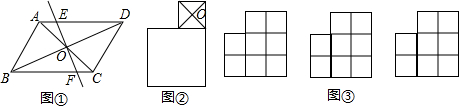
13��֪ʶ�����������ĶԳ�ͼ�εĶԳ����ĵ�����һ��ֱ�߶�����ֳ�ȫ�ȵ��������֣���1����ͼ�٣�ֱ��m����ƽ���ı���ABCD�Խ��ߵĽ���O����S�ı���AEFB=S�ı���DEFC���������������=������
��2����ͼ�ڣ�������������ͼ��ʾ�ڷţ�OΪС�����ζԽ��ߵĽ��㣬��������O��ֱ�߽�����ͼ�ηֳ������ȵ������֣�
��3���˸���С��ͬ����������ͼ����ʾ�ڷţ�����ֱ�߽�����ͼ�ηֳ������ȵ������֣������ַ����ַָ��
���� ��1������֪ʶ����������⣻
��2�����ҵ��������ε����ģ�Ȼ���������ֱ���ɣ�
��3���ȷֳ��������Σ��ҵ����ģ�Ȼ���������ֱ���ɣ�
��� �⣺��1����ͼ�٣�ֱ��m����ƽ���ı���ABCD�Խ��ߵĽ���O����S�ı���AEFB=S�ı���DEFC��
��2����ͼ��ʾ��
��3����ͼ��ʾ��
�ʴ�Ϊ��=��
���� ���⿼�����ĶԳƼ����ε����ʣ���һ���Ѷȣ�ע���������������ĶԳƵ�֮��Ĺ�ϵ��

��ϰ��ϵ�д�
 ����νӽ̲���ĩ���Ԥϰ�人������ϵ�д�
����νӽ̲���ĩ���Ԥϰ�人������ϵ�д� ������ҵ��ٳɳ����½������������ϵ�д�
������ҵ��ٳɳ����½������������ϵ�д�
�����Ŀ
6�������4x3y+2x4y2����E=-2-xy����ôE=��������
| A�� | -2x | B�� | 3x | C�� | -2x2 | D�� | -2x3y |
7���Ѻ���y=3x+2��ͼ������ƽ��1����λ���ȣ�����ͼ��ĺ�������ʽ�ǣ�������
| A�� | y=3x+3 | B�� | y=3x-1 | C�� | y=3x+1 | D�� | y=3x+5 |
8��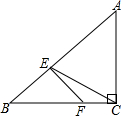 ��ͼ���ڡ�ABC�У�AC=BC����BCA=90�㣬��E��б��AB�ϵ�һ�㣬��EF��AB����BC�ڵ�F����EC����BE��EA=1��2�����ECF������ֵΪ��������
��ͼ���ڡ�ABC�У�AC=BC����BCA=90�㣬��E��б��AB�ϵ�һ�㣬��EF��AB����BC�ڵ�F����EC����BE��EA=1��2�����ECF������ֵΪ��������
 ��ͼ���ڡ�ABC�У�AC=BC����BCA=90�㣬��E��б��AB�ϵ�һ�㣬��EF��AB����BC�ڵ�F����EC����BE��EA=1��2�����ECF������ֵΪ��������
��ͼ���ڡ�ABC�У�AC=BC����BCA=90�㣬��E��б��AB�ϵ�һ�㣬��EF��AB����BC�ڵ�F����EC����BE��EA=1��2�����ECF������ֵΪ��������| A�� | $\frac{2\sqrt{5}}{5}$ | B�� | $\frac{\sqrt{5}}{5}$ | C�� | $\sqrt{5}$ | D�� | -$\frac{\sqrt{5}}{5}$ |
18�� ��ͼ��ֱ��l1��l2��l3��ֱ��AC�ֱ�l1��l2��l3�ڵ�A��B��C��ֱ��DF�ֱ�l1��
��ͼ��ֱ��l1��l2��l3��ֱ��AC�ֱ�l1��l2��l3�ڵ�A��B��C��ֱ��DF�ֱ�l1��
l2��l3�ڵ�D��E��F��AC��DF�ཻ�ڵ�H����AH=2��HB=1��BC=5����$\frac{DE}{EF}$��ֵΪ
��������
 ��ͼ��ֱ��l1��l2��l3��ֱ��AC�ֱ�l1��l2��l3�ڵ�A��B��C��ֱ��DF�ֱ�l1��
��ͼ��ֱ��l1��l2��l3��ֱ��AC�ֱ�l1��l2��l3�ڵ�A��B��C��ֱ��DF�ֱ�l1��l2��l3�ڵ�D��E��F��AC��DF�ཻ�ڵ�H����AH=2��HB=1��BC=5����$\frac{DE}{EF}$��ֵΪ
��������
| A�� | $\frac{1}{2}$ | B�� | 2 | C�� | $\frac{2}{5}$ | D�� | $\frac{3}{5}$ |
5�����и�ʽ�У���ȷ���� ��������
| A�� | $��\sqrt{9}=��3$ | B�� | -��$\sqrt{2}$��2=4 | C�� | $\root{3}{-9}=-3$ | D�� | $\sqrt{{{��-2��}^2}}=-2$ |
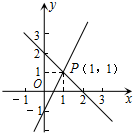 ��ͼ����֪����y=ax+b��y=kx��ͼ���ڵ�P�������ͼ��ɵã�����$\left\{\begin{array}{l}{y=ax+b}\\{y=kx}\end{array}\right.$�Ķ�Ԫһ�η�����Ľ���$\left\{\begin{array}{l}{x=1}\\{y=1}\end{array}\right.$��
��ͼ����֪����y=ax+b��y=kx��ͼ���ڵ�P�������ͼ��ɵã�����$\left\{\begin{array}{l}{y=ax+b}\\{y=kx}\end{array}\right.$�Ķ�Ԫһ�η�����Ľ���$\left\{\begin{array}{l}{x=1}\\{y=1}\end{array}\right.$��