题目内容
7.把函数y=3x+2的图象向下平移1个单位长度,所得图象的函数解析式是( )| A. | y=3x+3 | B. | y=3x-1 | C. | y=3x+1 | D. | y=3x+5 |
分析 直接利用一次函数平移规律,即k不变,进而利用一次函数图象上的性质得出答案.
解答 解:将函数y=3x+2的图象向下平移1个单位长度后,所得图象的函数关系式为y=3x+2-1=3x+1,
故选C.
点评 此题主要考查了一次函数平移,正确利用一次函数图象上点的坐标性质得出是解题关键.

练习册系列答案
相关题目
18.两个有理数的积是负数,和是零,那么这两个数( )
| A. | 都是负数 | |
| B. | 其中绝对值大的数是正数,另一个是负数 | |
| C. | 互为相反数 | |
| D. | 其中绝对值大的数是负数,另一个是正数 |
2.在-|-2|,|-(-3)|,-(+2),-(-$\frac{1}{2}$),+(-2),-(-3),-22中,负数有( )
| A. | 2个 | B. | 3个 | C. | 4个 | D. | 5个 |
12.若关于x的一元一次方程k(x+4)-2k-x=5的解为x=-3,则k的值是( )
| A. | -2 | B. | 2 | C. | $\frac{1}{5}$ | D. | -$\frac{1}{5}$ |
19.若$\frac{x}{y}$=$\frac{3}{2}$,则下列各式中成立的是( )
| A. | $\frac{x+y}{y}$=5 | B. | $\frac{y}{x-y}$=$\frac{1}{3}$ | C. | $\frac{x+3}{y+2}$=$\frac{2}{3}$ | D. | $\frac{x-y}{x+y}$=$\frac{1}{5}$ |
14.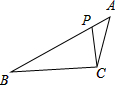 如图,已知是P是△ABC的边AB上一点,则在下列四个条件中,不能作为判定△ACP与△ABC相似条件的是( )
如图,已知是P是△ABC的边AB上一点,则在下列四个条件中,不能作为判定△ACP与△ABC相似条件的是( )
 如图,已知是P是△ABC的边AB上一点,则在下列四个条件中,不能作为判定△ACP与△ABC相似条件的是( )
如图,已知是P是△ABC的边AB上一点,则在下列四个条件中,不能作为判定△ACP与△ABC相似条件的是( )| A. | ∠ACP=∠B | B. | ∠APC=∠ACB | C. | $\frac{AP}{AC}$=$\frac{AC}{AB}$ | D. | $\frac{CP}{BC}$=$\frac{AC}{AB}$ |
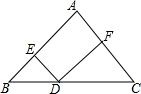 如图,已知点D在△ABC边BC上,且与B,D不重合,AC∥DE,AB∥DF,BC=5.
如图,已知点D在△ABC边BC上,且与B,D不重合,AC∥DE,AB∥DF,BC=5.