题目内容
10.阅读下面材料:在数学课上,老师请同学思考如下问题:如图,我们把一个四边形ABCD的四边中点E,F,G,H依次连接起来得到的四边形EFGH是平行四边形吗?
小敏在思考问题,有如下思路:连接AC.
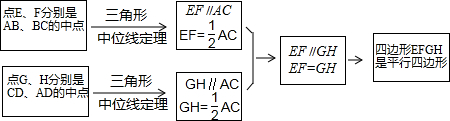
结合小敏的思路作答
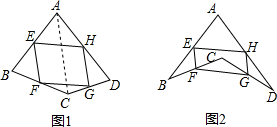
(1)若只改变图1中四边形ABCD的形状(如图2),则四边形EFGH还是平行四边形吗?说明理由;参考小敏思考问题方法解决以下问题:
(2)如图2,在(1)的条件下,若连接AC,BD.
①当AC与BD满足什么条件时,四边形EFGH是菱形,写出结论并证明;
②当AC与BD满足什么条件时,四边形EFGH是矩形,直接写出结论.
分析 (1)连接AC,根据三角形中位线的性质得到EF∥AC,EF=$\frac{1}{2}$AC,然后根据平行四边形判定定理即可得到结论;
(2)①由三角形中位线定理得出FG=HG,即可得出结论;
②根据平行线的性质得到GH⊥BD,GH⊥GF,于是得到∠HGF=90°,根据矩形的判定定理即可得到结论
解答 解:(1)四边形EFGH是平行四边形, 理由如下:
理由如下:
如图2,连接AC,
∵E是AB的中点,F是BC的中点,
∴EF∥AC,EF=$\frac{1}{2}$AC,
同理HG∥AC,HG=$\frac{1}{2}$AC,
综上可得:EF∥HG,EF=HG,
故四边形EFGH是平行四边形;
(2)①当AC=BD时,四边形EFGH为菱形;理由如下:
由(1)得:FG=$\frac{1}{2}$BD,HG=$\frac{1}{2}$AC,
当AC=BD时,FG=HG,
∴四边形EFGH为菱形;
②当AC⊥BD时,四边形EFGH为矩形;
理由如下:
同(1)得:四边形EFGH是平行四边形,
∵AC⊥BD,GH∥AC,
∴GH⊥BD,
∵GF∥BD,
∴GH⊥GF,
∴∠HGF=90°,
∴四边形EFGH为矩形.
点评 此题是四边形综合题目,主要考查了中点四边形、三角形中位线定理、平行四边形的判定、菱形的判定、矩形的判定等知识;本题综合性强,有一定难度,熟练掌握三角形中位线定理是解决问题的关键.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
15.刚刚过去的2017年春运总里程达到12亿千米,约等于地球到太阳距离的8倍,用科学记数法表示12亿为( )
| A. | 1.2×109 | B. | 1.2×108 | C. | 12×109 | D. | 12×108 |
2.下列雪花的图案中,包含了轴对称、旋转、位似三种变换的是( )
| A. |  | B. |  | C. |  | D. |  |







