题目内容
7.甲乙两地相距60km,一辆汽车好一辆摩托车同由两地相向而行,1小时20分钟相遇,相遇后,摩托车继续前进,汽车在相遇处停留1小时后调转车头原速返回,半小时后汽车追上了摩托车,求汽车和摩托车的速度各是多少?分析 设汽车的速度是x千米每小时,摩托车速度y千米每小时,根据“甲乙两地相距60km”、“相向而行,1小时20分钟相遇,相遇后,摩托车继续前进,汽车在相遇处停留1小时后调转车头原速返回,半小时后汽车追上了摩托车”列出方程,求出x,y的值,再根据路程=速度×时间即可得出答案.
解答 解:设汽车的速度是x千米每小时,摩托车速度y千米每小时,根据题意得:
$\left\{\begin{array}{l}{\frac{4}{3}(x+y)=60}\\{\frac{1}{2}x=\frac{3}{2}y}\end{array}\right.$,
解得:$\left\{\begin{array}{l}{x=\frac{135}{4}}\\{y=\frac{45}{4}}\end{array}\right.$,
答:汽车的速度是$\frac{135}{4}$千米/时,摩托车速度$\frac{45}{4}$千米/时.
点评 本题主要考查了二元一次方程组的应用的知识点,解题关键是要读懂题目的意思,根据题目给出的条件,找出合适的等量关系,列出方程组,再求解.利用二元一次方程组求解的应用题一般情况下题中要给出2个等量关系,准确的找到等量关系并用方程组表示出来是解题的关键;本题用到的知识点是路程=速度×时间.

练习册系列答案
 永乾教育寒假作业快乐假期延边人民出版社系列答案
永乾教育寒假作业快乐假期延边人民出版社系列答案
相关题目
17.下列计算正确的是( )
| A. | 2x•x=2x2 | B. | 2x2-3x2=-1 | C. | 6x6÷2x2=3x3 | D. | 2x+x=2x2 |
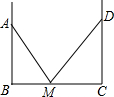 如图,装修师傅装修一间房子,在两墙之间有一个底端在点M的梯子,当它靠在一侧墙上时,梯子的顶端在点A,当它靠在另一侧墙上时,梯子的顶端在点D,已知∠AMB=55°,∠DMC=44°,点A到地面的垂直距离为4m,求点D到地面垂直的距离.(参考数据:sin55°≈0.8192,sin44°≈0.6947)
如图,装修师傅装修一间房子,在两墙之间有一个底端在点M的梯子,当它靠在一侧墙上时,梯子的顶端在点A,当它靠在另一侧墙上时,梯子的顶端在点D,已知∠AMB=55°,∠DMC=44°,点A到地面的垂直距离为4m,求点D到地面垂直的距离.(参考数据:sin55°≈0.8192,sin44°≈0.6947) 某校为培育青少年科技创新能力,举办了动漫制作活动,小华设计了点沿线段往返运动的一个雏形,甲以3cm/s的速度从A出发到B在返回到A,同时乙以每小时4cm/s的速度从B出发到A在返回到B.A,B的距离为21cm.
某校为培育青少年科技创新能力,举办了动漫制作活动,小华设计了点沿线段往返运动的一个雏形,甲以3cm/s的速度从A出发到B在返回到A,同时乙以每小时4cm/s的速度从B出发到A在返回到B.A,B的距离为21cm.