题目内容
6.阅读理解与运用.例 解分式不等式:$\frac{3x+2}{x-1}$>2.
解:移项,得:$\frac{3x+2}{x-1}$-2>0,即$\frac{x+4}{x-1}$>0.
由同号得正、异号得负的原理得,两种情况:①$\left\{\begin{array}{l}{x+4>0}\\{x-1>0}\end{array}\right.$;②$\left\{\begin{array}{l}{x+4<0}\\{x-1<0}\end{array}\right.$.
解不等式组①得:x>1;解不等式组②得:x<-4.∴原不等式的解集是:x<-4或x>1.
试运用上述方法解分式不等式:$\frac{x+2}{x-1}$<$\frac{1}{1-x}$.
分析 不等式整理后,转化为不等式组,求出解集即可.
解答 解:不等式整理得:$\frac{x+2}{x-1}$+$\frac{1}{x-1}$<0,即$\frac{x+3}{x-1}$<0,
由同号得正,异号得负得:$\left\{\begin{array}{l}{x+3<0}\\{x-1>0}\end{array}\right.$或$\left\{\begin{array}{l}{x+3>0}\\{x-1<0}\end{array}\right.$,
不等式组无解或-3<x<1,
则原不等式的解集为-3<x<1.
点评 此题考查了解一元一次不等式组,熟练掌握运算法则是解本题的关键.

练习册系列答案
相关题目
16.下列标志既是轴对称图形又是中心对称图形的是( )
| A. |  | B. |  | C. |  | D. |  |
11.设方程组$\left\{\begin{array}{l}{y=1-x}\\{3x+2y=5}\end{array}\right.$的解是M,则( )
| A. | M是方程y=1-x的唯一解 | B. | M是方程3x+2y=5的唯一解 | ||
| C. | M是方程3y-2x=-12的一个解 | D. | M不是方程3y-2x=-12的一个解 |
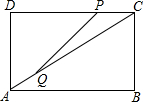 如图,在矩形ABCD中,AB=8厘米,BC=6厘米,点P从点C沿CD方向向终点D移动,同时点Q从点A沿AC方向向终点C移动,速度均为每秒1厘米,当一点到达终点时,另一点也停止运动
如图,在矩形ABCD中,AB=8厘米,BC=6厘米,点P从点C沿CD方向向终点D移动,同时点Q从点A沿AC方向向终点C移动,速度均为每秒1厘米,当一点到达终点时,另一点也停止运动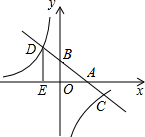 如图,在平面直角坐标系中,一次函数y=kx+b的图象分別交x轴、y轴于A、B两点.与反比例函数y=-$\frac{6}{x}$的图象交于C,D两点,DE⊥x轴于点E.已知DE=3,AE=6.
如图,在平面直角坐标系中,一次函数y=kx+b的图象分別交x轴、y轴于A、B两点.与反比例函数y=-$\frac{6}{x}$的图象交于C,D两点,DE⊥x轴于点E.已知DE=3,AE=6.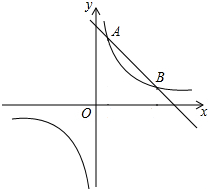 如图,直线y1=-x+b与双曲线y2=$\frac{8}{x}$交于A、B两点,点A的横坐标为1,则不等式-x+b<$\frac{8}{x}$的解集是0<x<1或x>8.
如图,直线y1=-x+b与双曲线y2=$\frac{8}{x}$交于A、B两点,点A的横坐标为1,则不等式-x+b<$\frac{8}{x}$的解集是0<x<1或x>8.