题目内容
18.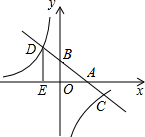 如图,在平面直角坐标系中,一次函数y=kx+b的图象分別交x轴、y轴于A、B两点.与反比例函数y=-$\frac{6}{x}$的图象交于C,D两点,DE⊥x轴于点E.已知DE=3,AE=6.
如图,在平面直角坐标系中,一次函数y=kx+b的图象分別交x轴、y轴于A、B两点.与反比例函数y=-$\frac{6}{x}$的图象交于C,D两点,DE⊥x轴于点E.已知DE=3,AE=6.(1)求一次函数的解析式;
(2)直接写出不等式kx+b+$\frac{6}{x}$>0的解集.
分析 (1)根据点D在反比例函数上,且DE=3可得出点D的坐标,再由AE=6可得出点A的坐标,由待定系数法即可求出直线AD的函数解析式;
(2)将一次函数解析式代入反比例函数中得处关于x的分式方程,解方程即可得出交点C的坐标,将原不等式进行变形,再结合一次函数与反比例函数图象可直接得出不等式的解集.
解答 解:(1)∵点D在反比例函数y=-$\frac{6}{x}$的图象上,且DE=3,
∴将y=3代入反比例函数解析式得:3=-$\frac{6}{x}$,即x=-2,
点D的坐标为(-2,3).
又∵AE=6,
∴A点的坐标为(4,0).
将A与D点的坐标代入一次函数解析式中得:$\left\{\begin{array}{l}{-2k+b=3}\\{4k+b=0}\end{array}\right.$,
解得:$\left\{\begin{array}{l}{k=-\frac{1}{2}}\\{b=2}\end{array}\right.$.
∴一次函数解析式为y=-$\frac{1}{2}$x+2.
(2)将y=-$\frac{1}{2}$x+2代入y=-$\frac{6}{x}$中得:-$\frac{1}{2}$x+2=-$\frac{6}{x}$,
解得:x1=-2,x2=6,
当x=6时,y=-$\frac{6}{6}$=-1,
即点C的坐标为(6,-1).
kx+b+$\frac{6}{x}$>0可转化为kx+b>-$\frac{6}{x}$,
根据两个函数y=-$\frac{1}{2}$x+2与y=-$\frac{6}{x}$的图象可知:
不等式的解集为:x<-2或0<x<6.
点评 本题考查了一次函数与反比例函数交点问题、待定系数法求函数解析式以及解分式方程,解题的关键:(1)利用待定系数法求函数解析式;(2)求出C点的坐标.本题属于基础题,难度不大,解决该题型题目时,根据给定条件求出函数解析式,再结合图象可直接得出不等式的解集.

 如图是一个正方体的表面展开图,则原正方体中与“和”字所在的面相对的面上标的字是( )
如图是一个正方体的表面展开图,则原正方体中与“和”字所在的面相对的面上标的字是( )| A. | 谐 | B. | 强 | C. | 富 | D. | 主 |
| A. | 三角形按边可分为不等边三角形,等腰三角形和等边三角形 | |
| B. | 等腰三角形任一个内角都有可能是钝角或直角 | |
| C. | 三角形的一个外角大于任何一个内角 | |
| D. | 三角形三条内角平分线相交于一点,这点到三角形三边的距离相等 |
 如图,AB∥CD,BD=CD,若∠C=40°,则∠ABD的度数为( )
如图,AB∥CD,BD=CD,若∠C=40°,则∠ABD的度数为( )| A. | 40° | B. | 60° | C. | 80° | D. | 120° |
| A. | $\frac{1}{18}$ | B. | $\frac{1}{12}$ | C. | $\frac{1}{9}$ | D. | $\frac{1}{6}$ |