题目内容
14.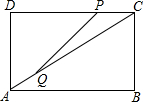 如图,在矩形ABCD中,AB=8厘米,BC=6厘米,点P从点C沿CD方向向终点D移动,同时点Q从点A沿AC方向向终点C移动,速度均为每秒1厘米,当一点到达终点时,另一点也停止运动
如图,在矩形ABCD中,AB=8厘米,BC=6厘米,点P从点C沿CD方向向终点D移动,同时点Q从点A沿AC方向向终点C移动,速度均为每秒1厘米,当一点到达终点时,另一点也停止运动(1)设运动的时间t秒,当t为何值时,△CPQ与△ACD相似?
(2)设四边形ADPQ的面积为S,当t为何值时,S有最小值?
分析 (1)分两种情况:①当PQ∥AD时,△QCP∽△ACD;②当PQ⊥AC时,△PCQ∽△ACD;即可求出答案;
(2)过点P作PM⊥BC于M,根据相似三角形的判定得出△PCM∽△ACD,求出PM,根据S等于△ABC的面积减去△PQC的面积,代入求出即可.
解答 解:(1)分两种情况:①PQ∥AD,如图1,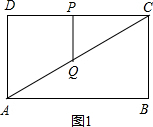
∴△QCP∽△ACD,
∴$\frac{PC}{CD}$=$\frac{CQ}{AC}$,
∵AB=8厘米,BC=6厘米,∠D=90°,
∴CP=t,CQ=10-t,AC=10厘米,
∴$\frac{t}{8}$=$\frac{10-t}{10}$,
∴t=$\frac{40}{9}$;
②当PQ⊥AC时,如图2,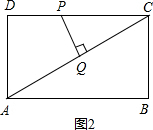
∴△PCQ∽△ACD;
∴$\frac{CQ}{CD}$=$\frac{CP}{CA}$,
∵AB=8厘米,BC=6厘米,∠D=90°,
∴CP=t,CQ=10-t,AC=10厘米,
∴$\frac{10-t}{8}$=$\frac{t}{10}$,
∴t=$\frac{50}{9}$;
∴t=$\frac{40}{9}$或$\frac{50}{9}$时,△CPQ与△ACD相似;
(2)如图3,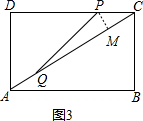
过P作PM⊥AC于M,
∵四边形ABCD为矩形,
∴∠D=∠B=∠PMC=90°,AD=BC=6,AB=DC=8,
在Rt△ADC中,由勾股定理得:AC=$\sqrt{A{B}^{2}+B{C}^{2}}$=$\sqrt{{8}^{2}+{6}^{2}}$=10,
∵∠PMC=∠D,∠PCM=∠DCA,
∴△PCM∽△ACD,
∴$\frac{PC}{AC}$=$\frac{PM}{AD}$,
∴$\frac{t×1}{10}$=$\frac{PM}{6}$,
解得:PM=$\frac{3}{5}$t,
∵四边形ADPQ的面积为S,
∴S=S△ADC-S△PQC
=$\frac{1}{2}$×AD×DC-$\frac{1}{2}$×CQ×PM
=$\frac{1}{2}×6×8$-$\frac{1}{2}×$(10-t)×$\frac{3}{5}$t
=$\frac{3}{5}$t2-3t+24
=$\frac{3}{5}$(t-5)2+$\frac{33}{2}$,
∵a=$\frac{3}{5}$>0,
∴图象的开口向上,即有最小值,
当t为5时,S有最小值.
点评 本题考查了矩形的性质,相似三角形的性质和判定,二次函数的最值问题的应用,能综合运用知识点进行推理和计算是解此题的关键,题目比较好,难度偏大.

| A. | 4a+c=9 | B. | 2a+c=9 | C. | 4a-c=9 | D. | 2a-c=9 |
 如图是一个正方体的表面展开图,则原正方体中与“和”字所在的面相对的面上标的字是( )
如图是一个正方体的表面展开图,则原正方体中与“和”字所在的面相对的面上标的字是( )| A. | 谐 | B. | 强 | C. | 富 | D. | 主 |
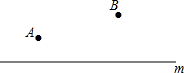 如图,某地由于居民增多,要在公路m上增加一个公共汽车站,A,B是路边两个新建小区,这个公共汽车站建在什么位置,能使两个小区到车站的路程一样长?(保留作图痕迹,不写作法)
如图,某地由于居民增多,要在公路m上增加一个公共汽车站,A,B是路边两个新建小区,这个公共汽车站建在什么位置,能使两个小区到车站的路程一样长?(保留作图痕迹,不写作法)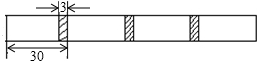 如图,将长为30cm、宽相等的长方形白纸,按如图所示的方法粘合起来,粘合部分的宽为3cm.则x张白纸粘合后的总长度为27x+3cm(用含x的代数式表示).
如图,将长为30cm、宽相等的长方形白纸,按如图所示的方法粘合起来,粘合部分的宽为3cm.则x张白纸粘合后的总长度为27x+3cm(用含x的代数式表示). 作图题
作图题