题目内容
1.已知某矩形的面积为20cm2.(1)写出其长y与宽x之间的函数表达式;
(2)如果要求矩形的长不小于8cm,其宽应满足什么条件?请说明理由.
分析 (1)利用矩形的面积公式列出两个变量之间的函数关系即可;
(2)根据其增减性确定宽的取值范围即可.
解答 解:(1)∵xy=20,
∴y=$\frac{20}{x}$;
(2)∵y=8时,x=2.5,
∴当矩形的长不小于8cm,其宽应满足0<x≤2.5.
点评 本题考查了反比例函数的应用,解题的关键是根据题意列出两个变量之间的函数关系式,难度不大.

练习册系列答案
 桃李文化快乐暑假武汉出版社系列答案
桃李文化快乐暑假武汉出版社系列答案 优秀生快乐假期每一天全新寒假作业本系列答案
优秀生快乐假期每一天全新寒假作业本系列答案 暑假接力赛新疆青少年出版社系列答案
暑假接力赛新疆青少年出版社系列答案
相关题目
9. 如图是一个正方体的表面展开图,则原正方体中与“和”字所在的面相对的面上标的字是( )
如图是一个正方体的表面展开图,则原正方体中与“和”字所在的面相对的面上标的字是( )
 如图是一个正方体的表面展开图,则原正方体中与“和”字所在的面相对的面上标的字是( )
如图是一个正方体的表面展开图,则原正方体中与“和”字所在的面相对的面上标的字是( )| A. | 谐 | B. | 强 | C. | 富 | D. | 主 |
10.下列命题中真命题是( )
| A. | 三角形按边可分为不等边三角形,等腰三角形和等边三角形 | |
| B. | 等腰三角形任一个内角都有可能是钝角或直角 | |
| C. | 三角形的一个外角大于任何一个内角 | |
| D. | 三角形三条内角平分线相交于一点,这点到三角形三边的距离相等 |
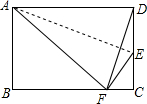 如图,点E为矩形ABCD的边CD上一点,将矩形ABCD沿AE折叠的一边,使点D落在BC边的点F处.若折痕$AE=5\sqrt{10},tan∠EFC=\frac{4}{3}$,则DF的长为3$\sqrt{10}$.
如图,点E为矩形ABCD的边CD上一点,将矩形ABCD沿AE折叠的一边,使点D落在BC边的点F处.若折痕$AE=5\sqrt{10},tan∠EFC=\frac{4}{3}$,则DF的长为3$\sqrt{10}$.