题目内容
7. 如图,顶角为36°的等腰三角形,其底边与腰之比等k,这样的三角形称为黄金三角形.已知腰AB=1,△ABC为第一个黄金三角形,△BCD为第二个黄金三角形,△CDE为第三个黄金三角形,以此类推,第2014个黄金三角形的周长( )
如图,顶角为36°的等腰三角形,其底边与腰之比等k,这样的三角形称为黄金三角形.已知腰AB=1,△ABC为第一个黄金三角形,△BCD为第二个黄金三角形,△CDE为第三个黄金三角形,以此类推,第2014个黄金三角形的周长( )| A. | k2013 | B. | k2014 | C. | $\frac{{k}^{2013}}{2+k}$ | D. | k2013(2+k) |
分析 根据相似三角形对应角相等,对应边成比例,求出前几个三角形的周长,进而找出规律:第n个黄金三角形的周长为kn-1(2+k),从而得出答案.
解答 解:∵AB=AC=1,
∴△ABC的周长为2+k;
△BCD的周长为k+k+k2=k(2+k);
△CDE的周长为k2+k2+k3=k2(2+k);
依此类推,第2014个黄金三角形的周长为k2013(2+k).
故选D.
点评 本题考查了黄金三角形,用到的知识点是黄金分割的定义和相似三角形的性质,找出各个三角形周长之间的关系,得出规律是本题的关键.

练习册系列答案
相关题目
15. 如图,是反比例函数y=$\frac{k_1}{x}$与反比例函数y=$\frac{k_2}{x}$(k1<k2)在第一象限的图象,直线AB∥x轴,并分别交两条曲线于A、B两点,若△AOB的面积是1,则k2-k1的值是( )
如图,是反比例函数y=$\frac{k_1}{x}$与反比例函数y=$\frac{k_2}{x}$(k1<k2)在第一象限的图象,直线AB∥x轴,并分别交两条曲线于A、B两点,若△AOB的面积是1,则k2-k1的值是( )
 如图,是反比例函数y=$\frac{k_1}{x}$与反比例函数y=$\frac{k_2}{x}$(k1<k2)在第一象限的图象,直线AB∥x轴,并分别交两条曲线于A、B两点,若△AOB的面积是1,则k2-k1的值是( )
如图,是反比例函数y=$\frac{k_1}{x}$与反比例函数y=$\frac{k_2}{x}$(k1<k2)在第一象限的图象,直线AB∥x轴,并分别交两条曲线于A、B两点,若△AOB的面积是1,则k2-k1的值是( )| A. | $\frac{1}{2}$ | B. | 1 | C. | $\frac{3}{2}$ | D. | 2 |
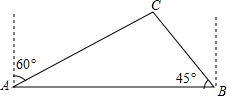 如图,某部门计划在火车站A和大学城B之间修一条长为4公里的公路,经测量在火车站A北偏东60度方向,B西偏北45度方向C处有一圆形公园,要想计划修筑的公路不会穿过公园,则公园半径最大为2($\sqrt{3}$-1)公里.
如图,某部门计划在火车站A和大学城B之间修一条长为4公里的公路,经测量在火车站A北偏东60度方向,B西偏北45度方向C处有一圆形公园,要想计划修筑的公路不会穿过公园,则公园半径最大为2($\sqrt{3}$-1)公里. 如图,DE是AC的垂直平分线,若AE=3cm,△ABD的周长是15cm,则△ABC的周长是21cm.
如图,DE是AC的垂直平分线,若AE=3cm,△ABD的周长是15cm,则△ABC的周长是21cm. 如图,∠A是⊙O的圆周角,∠A=60°,则∠BOC的度数为120°.
如图,∠A是⊙O的圆周角,∠A=60°,则∠BOC的度数为120°. 如图,已知EF过平行四边形ABCD的顶点C,分别交AB、AD的延长线于E、F,且DF=2cm,DA=5cm.BE=4cm.求CD的长.
如图,已知EF过平行四边形ABCD的顶点C,分别交AB、AD的延长线于E、F,且DF=2cm,DA=5cm.BE=4cm.求CD的长.