题目内容
12．解下列不等式，并把它的解集在数轴上表示出来．（1）3x-2（1-2x）≥1；
（2）$\frac{3x-4}{6}$＜$\frac{2x-1}{3}$．
分析 利用不等式的性质，先求出不等式的解集，再根据“大于向右，小于向左，包括端点用实心，不包括端点用空心”的原则将解集在数轴上表示出来．
解答 解：（1）3x-2（1-2x）≥1
3x-2+4x≥1
7x≥3
x≥$\frac{3}{7}$
把不等式的解集在数轴上表示为：
．
（2）$\frac{3x-4}{6}$＜$\frac{2x-1}{3}$
3x-4＜2（2x-1）
3x-4＜4x-2
-x＜2
x＞-2
把不等式的解集在数轴上表示为：
．
点评 此题考查解一元一次不等式，掌握方法与步骤是解决问题的关键．
练习册系列答案
同步轻松练习系列答案
课课通课程标准思维方法与能力训练系列答案
相关题目
2．代数式1-$\frac{{x}^{2}}{x}$是（ ）
| A． | 单项式 | B． | 多项式 | C． | 分式 | D． | 整式 |
3．
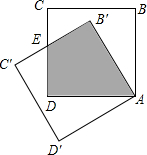如图，边长为1的正方形绕点A逆时针旋转30°得正方形AB′C′D′，则图中阴影部分面积为（ ）
如图，边长为1的正方形绕点A逆时针旋转30°得正方形AB′C′D′，则图中阴影部分面积为（ ）| A． | 1-$\frac{\sqrt{3}}{3}$ | B． | $\frac{\sqrt{3}}{3}$ | C． | $\frac{2\sqrt{3}}{3}$ | D． | 1-$\frac{2\sqrt{3}}{3}$ |
如图，点E为正方形ABCD的边BC延长线上一点，BF⊥DE于点F，交CD边于点G．
7．
如图，顶角为36°的等腰三角形，其底边与腰之比等k，这样的三角形称为黄金三角形．已知腰AB=1，△ABC为第一个黄金三角形，△BCD为第二个黄金三角形，△CDE为第三个黄金三角形，以此类推，第2014个黄金三角形的周长（ ）
如图，顶角为36°的等腰三角形，其底边与腰之比等k，这样的三角形称为黄金三角形．已知腰AB=1，△ABC为第一个黄金三角形，△BCD为第二个黄金三角形，△CDE为第三个黄金三角形，以此类推，第2014个黄金三角形的周长（ ）| A． | k2013 | B． | k2014 | C． | $\frac{{k}^{2013}}{2+k}$ | D． | k2013（2+k） |
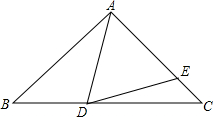如图，△ABC是等腰三角形，AB=AC，D、E分别是△ABC的边BC、AC上的点，且AD=AE，若∠BAD=46°，则∠EDC=23°．
如图，小李周末8时骑自行车从家里出发，到野外郊游，16时回到家里．他离开家后的距离S（千米）与时间t（时）的关系可以用图中的曲线表示．根据这个图象回答下列问题：