题目内容
3.小马虎在下面的计算中只做对了一道题,他做对的题目是( )| A. | (x+5)(y-5)=x-25 | B. | (x+y)2(x-y)2=x4-2x2y2+y4 | ||
| C. | 6m3÷(-3m2)•(2m)2=4m3 | D. | (8x3-4x2-2x)÷(-2x)=-4x2+2x |
分析 A、根据多项式乘多项式法则展开即可判断.
B、先用积的乘方公式,再利用完全平方公式展开即可判断.
C、根据同底数幂乘法、除法法则展开判断即可.
D、根据多项式除以单项式法则展开判断即可.
解答 解:A、(x-5)(y-5)=xy-5(x+y)+25,故错误.
B、(x+y)2(x-y)2=(x2-y2)2=x4-2x2y2+y4,故正确.
C、6m3÷(-3m2)•(2m)2=-4m3,故错误.
D、(8x3-4x2-2x)÷(-2x)=-4x2+2x+1,故错误.
故选B.
点评 本题考查整式的混合运算法则,熟练掌握整式的混合运算法则是解题的关键,注意运算符号,运算法则不能搞混淆,属于中考常考题型.

练习册系列答案
 53随堂测系列答案
53随堂测系列答案
相关题目
19.为了解当地气温变化情况,某研究小组记录了寒假期间连续4天的最高气温,结果如下(单位:℃):
5,-1,-3,-1.则下列结论错误的是( )
5,-1,-3,-1.则下列结论错误的是( )
| A. | 方差是8 | B. | 中位数是-1 | C. | 众数是-1 | D. | 平均数是0 |
11.下列说法正确的是( )
| A. | 4的平方根是2 | B. | 1的立方根是±1 | ||
| C. | $\sqrt{4}$的算术平方根是2 | D. | -1的立方根是-1 |
8.下列运算中正确的是( )
| A. | 3a+2a=5a2 | B. | -x2•(-x)3=(-x)5 | C. | 2a2•a3=2a6 | D. | (a-b)(b-a)=-(a-b)2 |
15.下列为二次根式的是( )
①$\sqrt{3}$,②$\sqrt{x}$(x>0),③$\sqrt{a}$,④$\sqrt{4}$-2,⑤$\sqrt{-4}$-2.
①$\sqrt{3}$,②$\sqrt{x}$(x>0),③$\sqrt{a}$,④$\sqrt{4}$-2,⑤$\sqrt{-4}$-2.
| A. | ①②③ | B. | ①②④ | C. | ②③⑤ | D. | ③④⑤ |
12.数学问题:在1~51这51个自然数中,每次取两个不同的数,使得所取的两个数之和大于51,有多少中不同取法?
数学模型:为找到解决上面问题的方法,先建立简单的数学模型进行研究:
(1)在1~5这5个自然数中,每次取两个不同的数,使得所取的两个数之和大于5,有多少种不同取法?
解决问题过程如下:
第1行有1种取法(1,5)
第2行有2种取法(2,4),(2,5)
第3行有3种取法(3,3),(3,4),(3,5)
第4行有4种取法(4,2),(4,3),(4,4),(4,5)
第5行有5种取法(5,1),(5,2),(5,3),(5,4),(5,5)
共有1+2+3+4+5种取法,因为每次取两个不同的数,所以在这些取法中不包括(3,3),(4,4),(5,5),要从总数中减去这3中取法,并且(4,2)与(2,4),(4,3)与(3,4),(5,1)与(1,5),(5,2)与(2,5),…(5,4)与(4,5)是同一种取法,因此共有$\frac{1+2+3+4+5-\frac{5+1}{2}}{2}$=6种不同的取法.
(2)在1~6这6个自然数中,每次取两个不同的数,使得所取的两个数之和大于6,有多少种不同的取法?
解决问题过程如下:
第1行有1种取法(1,6)
第2行有2种取法(2,5),(2,6)
第3行有3种取法(3,4),(3,5),(3,6)
第4行有4种取法(4,3),(4,4),(4,5),(4,6)
第5行有5种取法(5,2),(5,3),(5,4),(5,5),(5,6)
第6行有6种取法(6,1),(6,2),(6,3),6,4),(6,5),(6,6)
共有1+2+3+4+5+6种取法,因为每次取两个不同的数,所以在这些取法中不包括(4,4),(5,5),(6,6),要从总数中减去这3中取法,并且(4,3)与(3,4),(5,2)与(2,5),(5,3)与(3,5),(5,4)与(4,5),(6,1)与(1,6),(6,2)与(2,6)…(6,5)与(5,6)是同一种取法,因此共有$\frac{1+2+3+4+5+6-\frac{6}{2}}{2}$=9种不同的取法.
归纳探究:
仿照上述研究问题的思路和解决过程,回答下列提出的问题:
(1)在1~7这7个自然数中,每次取两个不同的数,使得所取的两个数之和大于7,共有12种不同取法.(只填结果)
(2)在1~8这8个自然数中,每次取两个不同的数,使得所取的两个数之和大于8,共有16种不同取法.(只填结果)
(3)在1~n(n为奇数)这n个自然数中,每次取两个不同的数,使得所取的两个数之和大于n,共有$\frac{{n}^{2}-1}{4}$种不同取法.(只填最简算式)
(4)在1~n(n为偶数)这n个自然数中,每次取两个不同的数,使得所取的两个数之和大于n,共有$\frac{{n}^{2}}{4}$种不同取法.(只填最简算式)
类比应用:类比上述研究方法或应用其结论,解决下列提出的问题:
(5)各边长都是整数,最大边长为51的三角形有多少个?(直接列出算术,并计算结果)
数学模型:为找到解决上面问题的方法,先建立简单的数学模型进行研究:
(1)在1~5这5个自然数中,每次取两个不同的数,使得所取的两个数之和大于5,有多少种不同取法?
解决问题过程如下:
| 1 | 2 | 3 | 4 | 5 | |
| 1 | (1,1) | (1,2) | (1,3) | (1,4) | (1,5) |
| 2 | (2,1) | (2,2) | (2,3) | (2,4) | (2,5) |
| 3 | (3,1) | (3,2) | (3,3) | (3,4) | (3,5) |
| 4 | (4,1) | (4,2) | (4,3) | (4,4) | (4,5) |
| 5 | (5,1) | (5,2) | (5,3) | (5,4) | (5,5) |
第2行有2种取法(2,4),(2,5)
第3行有3种取法(3,3),(3,4),(3,5)
第4行有4种取法(4,2),(4,3),(4,4),(4,5)
第5行有5种取法(5,1),(5,2),(5,3),(5,4),(5,5)
共有1+2+3+4+5种取法,因为每次取两个不同的数,所以在这些取法中不包括(3,3),(4,4),(5,5),要从总数中减去这3中取法,并且(4,2)与(2,4),(4,3)与(3,4),(5,1)与(1,5),(5,2)与(2,5),…(5,4)与(4,5)是同一种取法,因此共有$\frac{1+2+3+4+5-\frac{5+1}{2}}{2}$=6种不同的取法.
(2)在1~6这6个自然数中,每次取两个不同的数,使得所取的两个数之和大于6,有多少种不同的取法?
解决问题过程如下:
| 1 | 2 | 3 | 4 | 5 | 6 | |
| 1 | (1,1) | (1,2) | (1,3) | (1,4) | (1,5) | (1,6) |
| 2 | (2,1) | (2,2) | (2,3) | (2,4) | (2,5) | (2,6) |
| 3 | (3,1) | (3,2) | (3,3) | (3,4) | (3,5) | (3,6) |
| 4 | (4,1) | (4,2) | (4,3) | (4,4) | (4,5) | (4,6) |
| 5 | (5,1) | (5,2) | (5,3) | (5,4) | (5,5) | (5,6) |
| 6 | (6,1) | (6,2) | (6,3) | (6,4) | (6,5) | (6,6) |
第2行有2种取法(2,5),(2,6)
第3行有3种取法(3,4),(3,5),(3,6)
第4行有4种取法(4,3),(4,4),(4,5),(4,6)
第5行有5种取法(5,2),(5,3),(5,4),(5,5),(5,6)
第6行有6种取法(6,1),(6,2),(6,3),6,4),(6,5),(6,6)
共有1+2+3+4+5+6种取法,因为每次取两个不同的数,所以在这些取法中不包括(4,4),(5,5),(6,6),要从总数中减去这3中取法,并且(4,3)与(3,4),(5,2)与(2,5),(5,3)与(3,5),(5,4)与(4,5),(6,1)与(1,6),(6,2)与(2,6)…(6,5)与(5,6)是同一种取法,因此共有$\frac{1+2+3+4+5+6-\frac{6}{2}}{2}$=9种不同的取法.
归纳探究:
仿照上述研究问题的思路和解决过程,回答下列提出的问题:
(1)在1~7这7个自然数中,每次取两个不同的数,使得所取的两个数之和大于7,共有12种不同取法.(只填结果)
(2)在1~8这8个自然数中,每次取两个不同的数,使得所取的两个数之和大于8,共有16种不同取法.(只填结果)
(3)在1~n(n为奇数)这n个自然数中,每次取两个不同的数,使得所取的两个数之和大于n,共有$\frac{{n}^{2}-1}{4}$种不同取法.(只填最简算式)
(4)在1~n(n为偶数)这n个自然数中,每次取两个不同的数,使得所取的两个数之和大于n,共有$\frac{{n}^{2}}{4}$种不同取法.(只填最简算式)
类比应用:类比上述研究方法或应用其结论,解决下列提出的问题:
(5)各边长都是整数,最大边长为51的三角形有多少个?(直接列出算术,并计算结果)
13.下列说法正确的是( )
| A. | 一个有理数的平方根有两个,它们互为相反数 | |
| B. | 一个有理数的立方根,不是正数就是负数 | |
| C. | 负数没有立方根 | |
| D. | 如果一个数的立方根等于这个数的算术平方根,则这个数一定是0或1 |
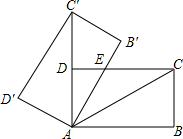 如图,将矩形ABCD绕点A旋转至矩形AB′C′D′位置,此时AC的中点恰好与D点重合,AB′交CD于点E.若DE=1,则矩形ABCD的面积为3$\sqrt{3}$.
如图,将矩形ABCD绕点A旋转至矩形AB′C′D′位置,此时AC的中点恰好与D点重合,AB′交CD于点E.若DE=1,则矩形ABCD的面积为3$\sqrt{3}$.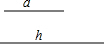 如图,已知两条线段的长度分别为a和h.
如图,已知两条线段的长度分别为a和h.