题目内容
5.为满足市场需求,某超市在春节来临前夕,购进一种品牌汤圆,每盒进价是20元,超市规定每盒售价不得少于25元.根据以往销售经验发现:当售价定为每盒25元时,每天可卖出350盒,每盒售价每提高1元,每天要少卖出10盒.(1)试求出每天的销售量y(盒)与每盒售价x(元)之间的函数关系式;
(2)当毎盒售价定为多少元时,每天销售的利润P(元)最大?最大利润是多少?
(3)为稳定物价,有关管理部门限定:这种汤圆的每盒售价不得高于35元.如果超市想要每天获得不低于3000元的利润,那么超市每天至少销售汤圆多少盒?
分析 (1)根据“当售价定为每盒25元时,每天可以卖出350盒,每盒售价每提高1元,每天要少卖出10盒”即可得出每天的销售量y(盒)与每盒售价x(元)之间的函数关系式;
(2)根据利润=1盒汤圆所获得的利润×销售量列式整理,再根据二次函数的最值问题解答;
(3)先由(2)中所求得的P与x的函数关系式,根据这种汤圆的每盒售价不得高于35元,且每天销售汤圆的利润不低于3000元,求出x的取值范围,再根据(1)中所求得的销售量y(盒)与每盒售价x(元)之间的函数关系式即可求解.
解答 解:(1)根据题意,y=350-10(x-25)=-10x+600;
(2)每天销售的利润P=(x-20)(-10x+600)=-10x2+800x-12000=-10(x-40)2+4000,
∴当x=40时,P取得最大值,最大值为4000,
答:当毎盒售价定为40元时,每天销售的利润P(元)最大,最大利润是4000元;
(3)根据题意得,-10(x-40)2+4000=3000,解得:x=30或x=50,
∴当30≤x≤50时,每天的销售利润不低于3000元,
又∵x≤35,
∴30≤x≤35,
在y=-10x+600中,y随x的增大而减小,
∴当x=35时,y最小值=-10×35+600=250,
即超市每天至少销售汤圆250盒.
点评 本题考查的是二次函数与一次函数在实际生活中的应用,主要利用了利润=1盒汤圆所获得的利润×销售量,求函数的最值时,注意自变量的取值范围.

练习册系列答案
相关题目
16.我省公布的居民用电电价听证方案如下:
例:某户月用电量400度,则需缴电费为210×0.55+(350-210)×(0.55+0.05)+(400-350)×(0.55+0.15)=234.5(元).
(1)如果按此方案计算,小华家5月份的电费为139.5元,请你求出小华家5月份的用电量;
(2)依据方案请你回答:若小华家某月的电费为248元,则小华家该月用电量是多少?属于第几档?
| 第一档电量 | 第二档电量 | 第三档电量 |
| 月用电量210度以下,每度价格0.55元 | 月用电量210度至350度,每度比第一档提价0.05元 | 月用电量350度以上,每度比第一档提价格0.15元 |
(1)如果按此方案计算,小华家5月份的电费为139.5元,请你求出小华家5月份的用电量;
(2)依据方案请你回答:若小华家某月的电费为248元,则小华家该月用电量是多少?属于第几档?
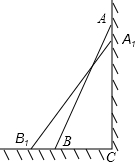 如图,一架2.5米长的梯子AB,斜靠在一竖直的墙AC上,这时梯子的顶端A到墙底端C的距离为2.4米,如果梯子的底端B沿CB向外平移0.8米至B1,求梯子顶端A沿墙下滑的距离AA1的长度.
如图,一架2.5米长的梯子AB,斜靠在一竖直的墙AC上,这时梯子的顶端A到墙底端C的距离为2.4米,如果梯子的底端B沿CB向外平移0.8米至B1,求梯子顶端A沿墙下滑的距离AA1的长度.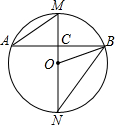 如图,MN是⊙O的直径,AB是⊙O的一条弦,且AB⊥MN于点C.
如图,MN是⊙O的直径,AB是⊙O的一条弦,且AB⊥MN于点C.