题目内容
10．一个底面半径是40cm，母线长为90cm的圆锥的侧面展开图的圆心角的度数为（ ）| A． | 80° | B． | 160° | C． | 320° | D． | 100° |
分析 根据圆锥的底面半径径求得圆锥的侧面展开扇形的弧长，再利用告诉的母线长求得圆锥的侧面展开扇形的面积，再利用扇形的另一种面积的计算方法求得圆锥的侧面展开图的圆心角即可．
解答 解：∵圆锥的底面半径是40cm，
∴圆锥的侧面展开扇形的弧长为：2πr=80π，
∵母线长90cm，
∴圆锥的侧面展开扇形的面积为：$\frac{1}{2}$lr=$\frac{1}{2}$×80π×90=3600π，
∴$\frac{nπ×9{0}^{2}}{360}$=3600π，
解得：n=160．
故选B．
点评 本题考查了圆锥的有关计算，解决此类题目的关键是明确圆锥的侧面展开扇形与圆锥的关系．
练习册系列答案
相关题目
如图，A（2，1），B（1，-1），以O为位似中心，按比例尺1：2，把△AOB放大，则点A的对应点A′的坐标为（4，2）或（-4，-2）．
1．
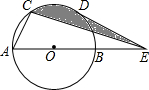如图所示，在半径为2cm的⊙O中，点C、点D是弧AB的三等分点，点E是直径AB的延长线上一点，连结CE、DE，则图中阴影部分的面积是（ ）
如图所示，在半径为2cm的⊙O中，点C、点D是弧AB的三等分点，点E是直径AB的延长线上一点，连结CE、DE，则图中阴影部分的面积是（ ）| A． | $\sqrt{3}$ | B． | $\frac{2π}{3}$ | C． | $\frac{2π}{3}-\sqrt{3}$ | D． | $\frac{2π}{3}$+$\sqrt{3}$ |
18．一组数据：3，4，5，6，6，的平均数、众数、中位数分别是（ ）
| A． | 4.8，6，6 | B． | 5，5，5 | C． | 4.8，6，5 | D． | 5，6，6 |
5．
如图，两个三角形的面积分别是9，6，对应阴影部分的面积分别是m，n，则m-n等于（ ）
如图，两个三角形的面积分别是9，6，对应阴影部分的面积分别是m，n，则m-n等于（ ）| A． | 2 | B． | 3 | C． | 4 | D． | 无法确定 |
15．在平面直角坐标系中，已知点A（-1，2），则点A关于x轴的对称点B的坐标是（ ）
| A． | （-1，-2） | B． | （1，2） | C． | （2，-1） |
2．为保障我国海外维和部队官兵的生活，现需通过A港口、B港口分别运送100吨和50吨生活物资．已知该物资在甲仓库存有80吨，乙仓库存有70吨，若从甲、乙两仓库运送物资到港口的费用（元/吨）如表所示：
（1）设从甲仓库运送到A港口的物资为x吨，求总运费y（元）与x（吨）之间的函数关系式，并写出x的取值范围；
（2）求出最低费用，并说明费用最低时的调配方案．
| 港口 | 运费（元/吨） | |
| 甲库 | 乙库 | |
| A港 | 14 | 20 |
| B港 | 10 | 8 |
（2）求出最低费用，并说明费用最低时的调配方案．
19．在-$\frac{1}{3}$，$\frac{1}{2013}$，-1，0这四个数中最小的是（ ）
| A． | -$\frac{1}{3}$ | B． | $\frac{1}{2013}$ | C． | -1 | D． | 0 |
20．化简：$\frac{x+3}{x+2}$-$\frac{x-2}{{x}^{2}-4}$=（ ）
| A． | $\frac{x+4}{x+2}$ | B． | 1 | C． | -1 | D． | $\frac{5}{{x}^{2}-4}$ |