��Ŀ����
6����ͼ��������y=-$\frac{1}{8}$x2+mx+n������ABC���������㣬��A������Ϊ��0��3������B������Ϊ��2��3������C��x���������ϣ���1����������ߵĺ�������ʽ����C�����ꣻ
��2����EΪ�߶�OC��һ���㣬��OEΪ���ڵ�һ��������������OEFG���������εĶ���Fǡ�������߶�AC��ʱ�����߶�OE�ij���
��3������2���е�������OEFG��OC����ƽ�ƣ���ƽ���е�������OEFGΪ������DEFG������E�͵�C�غ�ʱֹͣ�˶�����ƽ�Ƶľ���Ϊt��������DEFG�ı�EF��AC���ڵ�M��DG���ڵ�ֱ����AC���ڵ�N������DM���Ƿ����������t��ʹ��DMN�ǵ��������Σ������ڣ����tֵ���������ڣ���˵�����ɣ�
��4��������ƽ�ƹ����У���������DEFG���ABC���ص�����Ϊ�����ʱ����ֱ��д���ص����ֵ����S��ƽ�ƾ���t�ĺ�����ϵʽ���Ա���t��ȡֵ��Χ������tΪ��ֵʱ��S�����ֵ�����ֵ�Ƕ��٣�

���� ��1������������y=-$\frac{1}{8}$x2+mx+n������ABC���������㣬��A������Ϊ��0��3������B������Ϊ��2��3����������������ߵĽ���ʽ��
��2������������Ի�����Ӧ��ͼ�Σ�Ȼ����ݡ�AGF�ס�AOC���������OE�ij���������Խ����
��3���������⻭����Ӧ��ͼ�Σ�Ȼ����ݶ����������ƣ����Էֱ��ʾ��DM��MN��ND�ij���Ȼ�����÷������۵���ѧ˼����Խ���⣻
��4������������Ի�����Ӧ��ͼ�Σ�Ȼ�����ǰ������ĸ��ߵij��ȣ����Ա�ʾ���ص�������ε�������Ӷ��������S��t�ĺ�����ϵʽ���Լ�t��ȡֵ��Χ����tΪ��ֵʱ��S�����ֵ�����ֵ�Ƕ��٣�
���  �⣺��1����������y=-$\frac{1}{8}$x2+mx+n������ABC���������㣬��A������Ϊ��0��3������B������Ϊ��2��3����
�⣺��1����������y=-$\frac{1}{8}$x2+mx+n������ABC���������㣬��A������Ϊ��0��3������B������Ϊ��2��3����
��$\left\{\begin{array}{l}{n=3}\\{-\frac{1}{8}��{2}^{2}+m��2+n=3}\end{array}\right.$��
��ã�$\left\{\begin{array}{l}{m=\frac{1}{4}}\\{n=3}\end{array}\right.$
�������ߵĽ���ʽΪ��y�T-$\frac{1}{8}$x2+$\frac{1}{4}$x+3��
��������y=-$\frac{1}{8}$x2+mx+n������ABC���������㣬��C��x���������ϣ�
�ཫy=0����y�T-$\frac{1}{8}$x2+$\frac{1}{4}$x+3����x=-4��x=6��
���C��������6��0����
��2��������ɵã�����ͼһ��ʾ��
���ı���OEFG�������Σ�
��GF��OC��
���AGF�ס�AOC��
��$\frac{AG}{AO}=\frac{GF}{OC}$��
�ߵ�A��0��3������C��6��0����GF=OG����GF=a��
��$\frac{3-a}{3}=\frac{a}{6}$����a=2��
��OE=2��
��3�����ڣ���ͼ2
��EF��OA��
���MEC�ס�AOC��
��$\frac{ME}{AO}=\frac{CE}{CO}$����$\frac{ME}{3}=\frac{6-2-t}{6}$����ME=2-$\frac{t}{2}$��
��Rt��MED��$D{M}^{2}=D{E}^{2}+M{E}^{2}={2}^{2}+��2-\frac{t}{2}��^{2}$��
��DG��OA��
���CDN�ס�COA��
��$\frac{ND}{AO}=\frac{CD}{CO}$����$\frac{ND}{3}=\frac{6-t}{6}$����ND=3-$\frac{t}{2}$��
��M��MH��DG�ڵ�H����MH=2��DH=EM=2-$\frac{t}{2}$��
��$M{N}^{2}=M{H}^{2}+N{H}^{2}={2}^{2}+[��3-\frac{t}{2}��-��2-\frac{t}{2}��]^{2}$=5��
��DM=DNʱ��DM2=DN2��
��${2}^{2}+��2-\frac{t}{2}��^{2}=��3-\frac{t}{2}��^{2}$��
��ã�t=1��
��DN=NMʱ��DN2=MN2��
��$��3-\frac{t}{2}��^{2}=5$��
��ã�t=6-$2\sqrt{5}$��t=6+2$\sqrt{5}$����ȥ����
��DM=MNʱ��DM2=MN2��
��${2}^{2}+��2-\frac{t}{2}��^{2}=5$��
��ã�t=2��t=6����ȥ����
���Ͽɵã���t=2��t=1��t=6-$2\sqrt{5}$ʱ����DMN�ǵ��������Σ�
��4��������DEFG���ABC���ص�����Ϊ�����ʱ������ͼ3��ʾ�� �ɣ�3����֪��ME=2-$\frac{t}{2}$��DN=3-$\frac{t}{2}$��
�ɣ�3����֪��ME=2-$\frac{t}{2}$��DN=3-$\frac{t}{2}$��
��ֱ��BC�Ľ���ʽΪy=kx+b��
�ߵ�B��2��3������C��6��0��
��$\left\{\begin{array}{l}{2k+b=3}\\{6k+b=0}\end{array}\right.$����$\left\{\begin{array}{l}{k=-\frac{3}{4}}\\{b=\frac{9}{2}}\end{array}\right.$��
��ֱ��BC�Ľ���ʽΪy=$-\frac{3}{4}x+\frac{9}{2}$��
��ֱ��BC��EF���ڵ�K��
��OE=t+2��
�൱x=t+2ʱ��y=$-\frac{3}{4}x+\frac{9}{2}$=$-\frac{3}{4}��t+2��+\frac{9}{2}$=$-\frac{3}{4}t+3$��
���K��t+2��$-\frac{3}{4}t+3$����
��FK=2-��$-\frac{3}{4}t+3$��=$\frac{3}{4}t-1$��
��ֱ��BC��GF���ڵ�J��
���J����������2��
��y=2����y=$-\frac{3}{4}x+\frac{9}{2}$����x=$\frac{10}{3}$��
���J��������$\frac{10}{3}$��2����
��FJ=t+2-$\frac{10}{3}$=t-$\frac{4}{3}$��
��S=S������DEFG-S��FKJ-S����DEKN
=2��2-$\frac{1}{2}����\frac{3}{4}t-1����t-\frac{4}{3}��-$$\frac{1}{2}[��2-\frac{t}{2}��+��3-\frac{t}{2}��]��2$
=$-\frac{3}{8}{t}^{2}+2t-\frac{5}{3}$
=$-\frac{3}{8}��t-\frac{8}{3}��^{2}+1$��
��GH��y���ڵ�H����AC�ڵ�I���ɣ�2��֪��HI=2��
�֡�HJ=$\frac{10}{3}$��
��2$��t��\frac{10}{3}$��
��2��$\frac{8}{3}��\frac{10}{3}$��
�൱t=$\frac{8}{3}$ʱ��Sȡ�����ֵ�����ֵ��S=1��
���� ���⿼����κ����ۺ��⣬����Ĺؼ�����ȷ���⣬������Ŀ�и�������Ϣ������Ӧ��ͼ�Σ��ҳ�����������Ҫ���������������ν�ϵ�˼��ͷ������۵���ѧ˼�������⣬����һ���п�ѹ���⣬�������ϴ�һ��Ҫ��ϸ���森

 ���������ʱ��ѵϵ�д�
���������ʱ��ѵϵ�д� �㽭�¿γ���άĿ�������ʱ��ѵϵ�д�
�㽭�¿γ���άĿ�������ʱ��ѵϵ�д� ��������ϵ�д�
��������ϵ�д� ���ɶ���ܲ��¿�ֱͨ�߿�ϵ�д�
���ɶ���ܲ��¿�ֱͨ�߿�ϵ�д� ��������y=ax2+bx+c��ͼ��ʾ�������ĸ����ۣ�
��������y=ax2+bx+c��ͼ��ʾ�������ĸ����ۣ���abc��0����b-2a��0����a-b+c��0����b2-4ac��0��
������ȷ���۵ĸ����ǣ�������
| A�� | 1 | B�� | 2 | C�� | 3 | D�� | 4 |
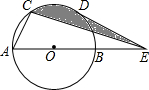 ��ͼ��ʾ���ڰ뾶Ϊ2cm�ġ�O�У���C����D�ǻ�AB�����ȷֵ㣬��E��ֱ��AB���ӳ�����һ�㣬����CE��DE����ͼ����Ӱ���ֵ�����ǣ�������
��ͼ��ʾ���ڰ뾶Ϊ2cm�ġ�O�У���C����D�ǻ�AB�����ȷֵ㣬��E��ֱ��AB���ӳ�����һ�㣬����CE��DE����ͼ����Ӱ���ֵ�����ǣ�������| A�� | $\sqrt{3}$ | B�� | $\frac{2��}{3}$ | C�� | $\frac{2��}{3}-\sqrt{3}$ | D�� | $\frac{2��}{3}$+$\sqrt{3}$ |
| A�� | �� | B�� | �� | C�� | �� | D�� | �� |
| A�� | 4.8��6��6 | B�� | 5��5��5 | C�� | 4.8��6��5 | D�� | 5��6��6 |
| A�� | ��-1��-2�� | B�� | ��1��2�� | C�� | ��2��-1�� |
 ��ѧϰ����ͼʱ����ʦ�ڽ�̨�����ĺз۱ʺаڷų���ͼ��״�ļ����壬��ô�ü����������ͼ��ȷ���ǣ�������
��ѧϰ����ͼʱ����ʦ�ڽ�̨�����ĺз۱ʺаڷų���ͼ��״�ļ����壬��ô�ü����������ͼ��ȷ���ǣ�������