题目内容
2.解不等式组,并把解集在数轴上表示出来:$\left\{{\begin{array}{l}\frac{x}{2}+4≤1\\ x-8>2(x+2)\end{array}}\right.$.分析 先求出不等式组中每一个不等式的解集,然后把不等式的解集表示在数轴上,再求出它们的公共部分即可.
解答 解:$\left\{\begin{array}{l}{\frac{x}{2}+4≤1…①}\\{x-8>2(x+2)…②}\end{array}\right.$,
解①得:x≤-6,
解②得:x<-12.
则不等式组的解集是:x<-12.
点评 本题考查的是一元一次不等式组的解,解此类题目常常要结合数轴来判断.还可以观察不等式的解,若x>较小的数、<较大的数,那么解集为x介于两数之间.

练习册系列答案
 名师伴你成长课时同步学练测系列答案
名师伴你成长课时同步学练测系列答案
相关题目
12.如图,EO⊥AB于点O,∠EOC=40°,则∠AOD=( )
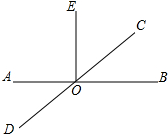

| A. | 30° | B. | 40° | C. | 50° | D. | 60° |
10.在下列各组单项式中,不是同类项的是( )
| A. | -$\frac{1}{2}$x2y和-yx2 | B. | -3和100 | C. | -x2yz和-xy2z | D. | -abc和$\frac{5}{2}$abc |
17. 如图,AD∥BC∥x轴,下列说法正确的是( )
如图,AD∥BC∥x轴,下列说法正确的是( )
 如图,AD∥BC∥x轴,下列说法正确的是( )
如图,AD∥BC∥x轴,下列说法正确的是( )| A. | A与D的横坐标相同 | B. | C与D的横坐标相同 | ||
| C. | B与C的纵坐标相同 | D. | B与D的纵坐标相同 |
7.已知一次函数y=-2x+2,点A(-1,a),B(-2,b)在该函数图象上,则a与b的大小关系是( )
| A. | a<b | B. | a>b | C. | a≥b | D. | a=b |
11.下列四个立体图形中,它们各自的三视图有两个相同,而另一个不同的是( )


| A. | ①② | B. | ②③ | C. | ②④ | D. | ③④ |
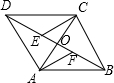 如图,在平行四边形ABCD中,对角线AC、BD相交于点O,点E、F分别是对角线BD上的点,且∠CEO=∠AFO,根据题上的条件能判定相等的线段共有( )
如图,在平行四边形ABCD中,对角线AC、BD相交于点O,点E、F分别是对角线BD上的点,且∠CEO=∠AFO,根据题上的条件能判定相等的线段共有( ) cm.
cm.