题目内容
4.已知二次函数y=x2-ax-2a2(a为常数,且a≠0).(1)证明该二次函数的图象与x轴的正半轴、负半轴各有一个交点;
(2)若该二次函数的图象与y轴的交点坐标为(0,-2),试求该函数图象的顶点坐标.
分析 (1)令y=0可求得方程的两个根一正一负,可证得结论;
(2)把(0,-2)代入抛物线的解析可求得a的值,进一步可求得其顶点坐标.
解答 (1)证明:
y=x2-ax-2a2=(x+a)(x-2a),
令y=0,则x1=-a,x2=2a,
∵a≠0,x1、x2的值必为一正一负,
∴该二次函数的图象与x轴的正半轴、负半轴各有一个交点;
(2)解:
由题意,得-2a2=-2,所以a=1或-1.
当a=1时,y=x2-x-2=(x-$\frac{1}{2}$)2-$\frac{9}{4}$,顶点坐标为($\frac{1}{2}$,-$\frac{9}{4}$),
当a=-1时,y=x2+x-2=(x+$\frac{1}{2}$)2-$\frac{9}{4}$,顶点坐标为(-$\frac{1}{2}$,-$\frac{9}{4}$),
该函数图象的顶点坐标为($\frac{1}{2}$,-$\frac{9}{4}$)或(-$\frac{1}{2}$,-$\frac{9}{4}$).
点评 本题主要考查二次函数与x轴的交点和顶点坐标,掌握二次函数与x轴交点的横坐标是对应一元二次方程的两根是解题的关键.

练习册系列答案
相关题目
3. 如图,线段AB两个端点的坐标分别为A(4,4),B(6,2),以原点O为位似中心,在第一象限内将线段AB缩小为原来的$\frac{1}{2}$后得到线段CD,则端点C和D的坐标分别为( )
如图,线段AB两个端点的坐标分别为A(4,4),B(6,2),以原点O为位似中心,在第一象限内将线段AB缩小为原来的$\frac{1}{2}$后得到线段CD,则端点C和D的坐标分别为( )
 如图,线段AB两个端点的坐标分别为A(4,4),B(6,2),以原点O为位似中心,在第一象限内将线段AB缩小为原来的$\frac{1}{2}$后得到线段CD,则端点C和D的坐标分别为( )
如图,线段AB两个端点的坐标分别为A(4,4),B(6,2),以原点O为位似中心,在第一象限内将线段AB缩小为原来的$\frac{1}{2}$后得到线段CD,则端点C和D的坐标分别为( )| A. | (2,2),(3,2) | B. | (2,4),(3,1) | C. | (2,2),(3,1) | D. | (3,1),(2,2) |
14.已知y是关于x的反比例函数,点P(x1,y1),Q(x2,y2)是反比例函数图象上的点,则下列结论正确的是( )
| A. | x1+y1=x2+y2 | B. | x1y2=x2y1 | C. | $\frac{{x}_{1}}{{x}_{2}}$=$\frac{{y}_{1}}{{y}_{2}}$ | D. | $\frac{{x}_{2}}{{x}_{1}}$=$\frac{{y}_{1}}{{y}_{2}}$ |
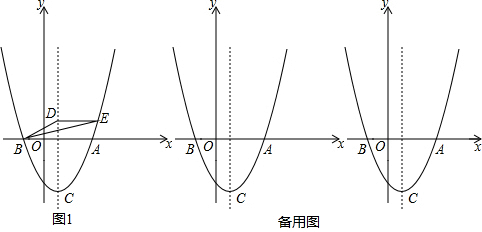
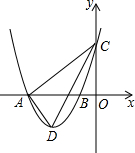 如图,在平面直角坐标系中,抛物线y=ax2+bx+3与x轴交于A(-4,0)、B(-l,0)两点,与y轴交于点C,点D是第三象限的抛物线上一动点.
如图,在平面直角坐标系中,抛物线y=ax2+bx+3与x轴交于A(-4,0)、B(-l,0)两点,与y轴交于点C,点D是第三象限的抛物线上一动点.