题目内容
13.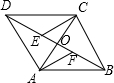 如图,在平行四边形ABCD中,对角线AC、BD相交于点O,点E、F分别是对角线BD上的点,且∠CEO=∠AFO,根据题上的条件能判定相等的线段共有( )
如图,在平行四边形ABCD中,对角线AC、BD相交于点O,点E、F分别是对角线BD上的点,且∠CEO=∠AFO,根据题上的条件能判定相等的线段共有( )| A. | 5对 | B. | 6对 | C. | 7对 | D. | 8对 |
分析 由平行四边形的性质可得到对边相等、对角线互相平分,再证明△CEO≌△AFO,可得到OE=OF、CE=AF,且容易得到DE=BF,可得到答案.
解答 解:
∵四边形ABCD为平行四边形,
∴AB=CD,AD=BC,OC=OA,OD=OB,
在△CEO△AFO中
$\left\{\begin{array}{l}{∠CEO=∠AFO}\\{∠COE=∠AOF}\\{OC=OA}\end{array}\right.$
∴△CEO≌△AFO(AAS),
∴CE=AF,OE=OF,
∵OD=OB,
∴DE=BF,
∴相等的线段共有七对,
故选C.
点评 本题主要考查平行四边形的性质,掌握平行四边形的性质是解题的关键,即平行四边形的对边平行且相等、对角相等、对角线互相平分.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
1.下列调查中,适宜采用全面调查方式的是( )
| A. | 了解某班学生对中国首辆月球车--“玉兔”的知晓情况 | |
| B. | 了解某市中学生每天体育锻炼的时间 | |
| C. | 了解某市市民对城市建设的满意度 | |
| D. | 了解南方人对雾霾危害的了解情况 |
3. 如图,线段AB两个端点的坐标分别为A(4,4),B(6,2),以原点O为位似中心,在第一象限内将线段AB缩小为原来的$\frac{1}{2}$后得到线段CD,则端点C和D的坐标分别为( )
如图,线段AB两个端点的坐标分别为A(4,4),B(6,2),以原点O为位似中心,在第一象限内将线段AB缩小为原来的$\frac{1}{2}$后得到线段CD,则端点C和D的坐标分别为( )
 如图,线段AB两个端点的坐标分别为A(4,4),B(6,2),以原点O为位似中心,在第一象限内将线段AB缩小为原来的$\frac{1}{2}$后得到线段CD,则端点C和D的坐标分别为( )
如图,线段AB两个端点的坐标分别为A(4,4),B(6,2),以原点O为位似中心,在第一象限内将线段AB缩小为原来的$\frac{1}{2}$后得到线段CD,则端点C和D的坐标分别为( )| A. | (2,2),(3,2) | B. | (2,4),(3,1) | C. | (2,2),(3,1) | D. | (3,1),(2,2) |
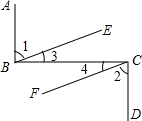 已知:如图AB⊥BC,BC⊥CD且∠1=∠2,试说明:BE∥CF.
已知:如图AB⊥BC,BC⊥CD且∠1=∠2,试说明:BE∥CF. 如图,数轴上标出若干个点,每个相邻两点距离相等,点A,B,C,D对应的数分别是数a,b,c,d,a+b+c+d=2,a-b+c-d=-3,求a点位置.
如图,数轴上标出若干个点,每个相邻两点距离相等,点A,B,C,D对应的数分别是数a,b,c,d,a+b+c+d=2,a-b+c-d=-3,求a点位置.