题目内容
14.若直角三角形三边长分别为6cm,8cm和xcm,则x=10cm或 cm.
cm.
分析 求第三边的长必须分类讨论,即8是斜边或直角边的两种情况,然后利用勾股定理求解.
解答 解:(1)若8是直角边,则第三边x是斜边,
由勾股定理得,62+82=x2
解得:x=10.
(2)若8是斜边,则第三边x为直角边,
由勾股定理得,62+x2=82,
解得x=2$\sqrt{7}$,
所以x的值为:10cm或2$\sqrt{7}$cm.
故答案为:10cm或2$\sqrt{7}$cm.
点评 本题考查了勾股定理解直角三角形,当已知条件中没有明确哪是斜边时,要注意分类讨论.

练习册系列答案
 轻松暑假总复习系列答案
轻松暑假总复习系列答案
相关题目
9.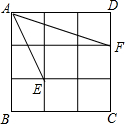 如图,正方形ABCD是由9个边长为1的小正方形组成,每个小正方形的顶点都叫格点,连接AE,AF,则∠EAF=( )
如图,正方形ABCD是由9个边长为1的小正方形组成,每个小正方形的顶点都叫格点,连接AE,AF,则∠EAF=( )
 如图,正方形ABCD是由9个边长为1的小正方形组成,每个小正方形的顶点都叫格点,连接AE,AF,则∠EAF=( )
如图,正方形ABCD是由9个边长为1的小正方形组成,每个小正方形的顶点都叫格点,连接AE,AF,则∠EAF=( )| A. | 30° | B. | 45° | C. | 60° | D. | 35° |
19.估计$\sqrt{40}-4$的值在( )
| A. | 2到3之间 | B. | 4到5之间 | C. | 6到7之间 | D. | 8到9之间 |
3. 如图,线段AB两个端点的坐标分别为A(4,4),B(6,2),以原点O为位似中心,在第一象限内将线段AB缩小为原来的$\frac{1}{2}$后得到线段CD,则端点C和D的坐标分别为( )
如图,线段AB两个端点的坐标分别为A(4,4),B(6,2),以原点O为位似中心,在第一象限内将线段AB缩小为原来的$\frac{1}{2}$后得到线段CD,则端点C和D的坐标分别为( )
 如图,线段AB两个端点的坐标分别为A(4,4),B(6,2),以原点O为位似中心,在第一象限内将线段AB缩小为原来的$\frac{1}{2}$后得到线段CD,则端点C和D的坐标分别为( )
如图,线段AB两个端点的坐标分别为A(4,4),B(6,2),以原点O为位似中心,在第一象限内将线段AB缩小为原来的$\frac{1}{2}$后得到线段CD,则端点C和D的坐标分别为( )| A. | (2,2),(3,2) | B. | (2,4),(3,1) | C. | (2,2),(3,1) | D. | (3,1),(2,2) |
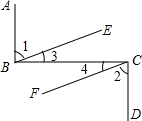 已知:如图AB⊥BC,BC⊥CD且∠1=∠2,试说明:BE∥CF.
已知:如图AB⊥BC,BC⊥CD且∠1=∠2,试说明:BE∥CF.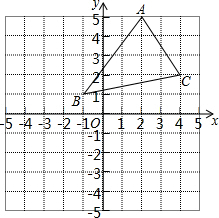 如图,将三角形ABC向左平移3个单位长度,再向下平移4个单位长度,得到三角形A′B′C′,且点A,B,C的对应点分别为点A′,B′,C′.
如图,将三角形ABC向左平移3个单位长度,再向下平移4个单位长度,得到三角形A′B′C′,且点A,B,C的对应点分别为点A′,B′,C′.