题目内容
12.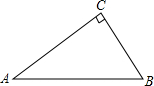 如图,某市把一块形状为直角三角形的废地开辟为生物园,∠ACB=90°,AC=80m,BC=60m.
如图,某市把一块形状为直角三角形的废地开辟为生物园,∠ACB=90°,AC=80m,BC=60m.(1)若入口E在边AB上,且与A、B距离相等,求从人口E到出口C的最短路线的长;
(2)若线段CD是一条水渠,且点D在AB边上,已知水渠造价约为10元/m,则点D在距点A多远处,此水渠的造价最低?最低造价是多少?
分析 (1)由题意可知:E点是AB的中点,则连接CE,CE是AB边的中线,则根据直角三角形中中线是斜边的一半;只要求得斜边AB的长即可,根据勾股定理可以求得AB的长;
(2)根据从一点到一直线垂线段线段的距离最短可知:从C点向AB作垂线,则CD的造价最低;根据三角形相似可以求得CD的长,AD的长;最后可以求得水渠的造价.
解答 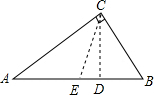 解:(1)过点C作CD⊥AB于D,取AB的中点为E,连接CE,
解:(1)过点C作CD⊥AB于D,取AB的中点为E,连接CE,
根据勾股定理可知:AB=$\sqrt{A{C}^{2}+B{C}^{2}}$=$\sqrt{8{0}^{2}+6{0}^{2}}$=100,
由题意可知:E点是AB的中点,
根据直角三角形中斜边上的中线是斜边的一半,
则CE=$\frac{1}{2}$AB=$\frac{1}{2}$×100=50m;
(2)由题意可知:从一点到一直线垂线段线段的距离最短,则从C点向AB作垂线,则CD的造价最低;
∵△ACB是直角三角形,CD⊥AB,
∴△ADC∽△ACB,
则$\frac{AC}{AB}$=$\frac{CD}{CB}$=$\frac{AD}{AC}$,
即$\frac{80}{100}$=$\frac{CD}{60}$=$\frac{AD}{80}$,
可解得:AD=64,CD=48;
则最低造价=10×48=480元.
答:点D在距点A64m处,此水渠的造价最低,最低造价是480元.
点评 本题考查的是勾股定理的应用,在应用勾股定理解决实际问题时勾股定理与方程的结合是解决实际问题常用的方法,关键是从题中抽象出勾股定理这一数学模型,画出准确的示意图.领会数形结合的思想的应用.

练习册系列答案
相关题目
3.一个三角形三边长度的比为3:4:5,最短的边比最短的边短6cm,则这个三角形的周长为( )
| A. | 30cm | B. | 36cm | C. | 39cm | D. | 33cm |
7.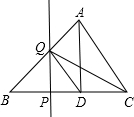 如图,△ABC中,AD⊥BC,垂足为D,AD=BD=3,CD=2,点P从点B出发沿线段BC的方向移动到点C停止,过点P作PQ⊥BC,交折线BA-AC于点Q,连接DQ、CQ,若△ADQ与△CDQ的面积相等,则线段BP的长度是( )
如图,△ABC中,AD⊥BC,垂足为D,AD=BD=3,CD=2,点P从点B出发沿线段BC的方向移动到点C停止,过点P作PQ⊥BC,交折线BA-AC于点Q,连接DQ、CQ,若△ADQ与△CDQ的面积相等,则线段BP的长度是( )
 如图,△ABC中,AD⊥BC,垂足为D,AD=BD=3,CD=2,点P从点B出发沿线段BC的方向移动到点C停止,过点P作PQ⊥BC,交折线BA-AC于点Q,连接DQ、CQ,若△ADQ与△CDQ的面积相等,则线段BP的长度是( )
如图,△ABC中,AD⊥BC,垂足为D,AD=BD=3,CD=2,点P从点B出发沿线段BC的方向移动到点C停止,过点P作PQ⊥BC,交折线BA-AC于点Q,连接DQ、CQ,若△ADQ与△CDQ的面积相等,则线段BP的长度是( )| A. | $\frac{9}{5}$或4 | B. | $\frac{6}{5}$或4 | C. | $\frac{9}{5}$或$\frac{13}{5}$ | D. | $\frac{6}{5}$或$\frac{13}{5}$ |
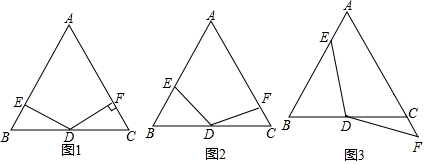
4. 如图,菱形纸片ABCD中,∠A=60°,将纸片折叠,点A,D分别落在A′,D′处,且A′D′经过点B,EF为折痕,当D′F⊥CD时,$\frac{CF}{BE}$的值为( )
如图,菱形纸片ABCD中,∠A=60°,将纸片折叠,点A,D分别落在A′,D′处,且A′D′经过点B,EF为折痕,当D′F⊥CD时,$\frac{CF}{BE}$的值为( )
 如图,菱形纸片ABCD中,∠A=60°,将纸片折叠,点A,D分别落在A′,D′处,且A′D′经过点B,EF为折痕,当D′F⊥CD时,$\frac{CF}{BE}$的值为( )
如图,菱形纸片ABCD中,∠A=60°,将纸片折叠,点A,D分别落在A′,D′处,且A′D′经过点B,EF为折痕,当D′F⊥CD时,$\frac{CF}{BE}$的值为( )| A. | $\frac{3-\sqrt{3}}{2}$ | B. | $\frac{3+\sqrt{3}}{2}$ | C. | $\frac{3-\sqrt{3}}{3}$ | D. | $\frac{3+\sqrt{3}}{3}$ |

 如图,ABCD是圆O的内接四边形,BC是圆O的直径,∠ACB=20°,D为弧$\widehat{AC}$的中点,求∠DAC的度数.
如图,ABCD是圆O的内接四边形,BC是圆O的直径,∠ACB=20°,D为弧$\widehat{AC}$的中点,求∠DAC的度数.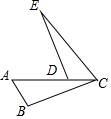 已知:如图,点A,D,C在同一直线上,AB∥EC,AC=CE,∠B=∠EDC.
已知:如图,点A,D,C在同一直线上,AB∥EC,AC=CE,∠B=∠EDC.