题目内容
1．
如图，ABCD是圆O的内接四边形，BC是圆O的直径，∠ACB=20°，D为弧$\widehat{AC}$的中点，求∠DAC的度数．
分析 根据圆周角定理得到∠BAC=90°，求出∠B，根据圆内接四边形的性质求出∠D=110°，根据圆心角、弧、弦三者的关系定理解答即可．
解答 解：∵BC为圆O的直径，
∴∠BAC=90°，
∴∠B=90°-200=700．
∵四边形ABCD为圆O内接四边形，
∴∠B+∠D=180°，
∴∠D=110°．
因为D为弧AC中点，
∴$\widehat{AD}$=$\widehat{CD}$，
∴∠DAC=35°．
点评 本题考查的是圆内接四边形的性质、圆周角定理的应用，掌握圆内接四边形的对角互补是解题的关键．
练习册系列答案
阅读快车系列答案
相关题目
如图，抛物线顶点坐标是P（1，2），函数y随自变量x的增大而减小的x的取值范围是x＞1．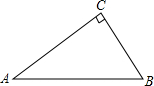
如图，某市把一块形状为直角三角形的废地开辟为生物园，∠ACB=90°，AC=80m，BC=60m．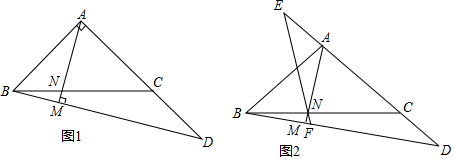
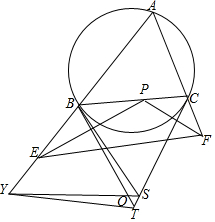如图，在△ABC中，∠A=60°，P为线段BC（不含端点）上一点，E、F分别为射线AB、AC上的点，且BP=BE，CP=CF，△ABC的外接圆在B、C两点处的切线交于点S．设△EPF的外心为O，BO与CS交于点T，SO与直线AB交于点Y．求证：B、Y、T、S四点共圆．
观察下列每对数在数轴上的对应点之间的距离：4与-2，3与5，-2与-6，-4与3．并回答下列各题：