题目内容
4.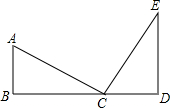 如图所示,点D为BC延长线上一点,点A,E是直线BC同侧的两点,∠B=90°,CD=AB,DE∥AB,AC⊥CE于C,求证:点C在线段AE的垂直平分线上.
如图所示,点D为BC延长线上一点,点A,E是直线BC同侧的两点,∠B=90°,CD=AB,DE∥AB,AC⊥CE于C,求证:点C在线段AE的垂直平分线上.
分析 根据已知条件可以证明△ABC≌△CDE,从而可以得到CA=EC,从而可以证明结论成立.
解答 证明:∵∠B=90°,DE∥AB,
∴∠B+∠D=180°
得∠D=90°,
∵AC⊥CE,∠A+∠BCA=90°,
∴∠ACE=90°,∠BCA+∠ECD=90°,
∴∠A=∠ECD,
在△ABC和△CDE中,
$\left\{\begin{array}{l}{∠A=∠ECD}\\{AB=CD}\\{∠B=∠D}\end{array}\right.$,
∴△ABC≌△CDE(ASA),
∴AC=CE,
∴点C在线段AE的垂直平分线上.
点评 本题考查全等三角形的判定与性质、线段垂直平分线的性质,解题的关键是证明△ABC≌△CDE.

练习册系列答案
 金牌教辅培优优选卷期末冲刺100分系列答案
金牌教辅培优优选卷期末冲刺100分系列答案
相关题目
5.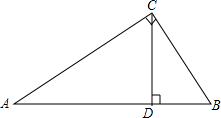 如图,在Rt△ABC中,∠C=90°,CD是斜边AB上的高,下列线段的比值不等于cosA的值的是( )
如图,在Rt△ABC中,∠C=90°,CD是斜边AB上的高,下列线段的比值不等于cosA的值的是( )
 如图,在Rt△ABC中,∠C=90°,CD是斜边AB上的高,下列线段的比值不等于cosA的值的是( )
如图,在Rt△ABC中,∠C=90°,CD是斜边AB上的高,下列线段的比值不等于cosA的值的是( )| A. | $\frac{AD}{AC}$ | B. | $\frac{AC}{AB}$ | C. | $\frac{BD}{BC}$ | D. | $\frac{CD}{BC}$ |
 如图,若
如图,若 所在位置的坐标为(-1,-2),
所在位置的坐标为(-1,-2), 所在的位置的坐标为(2,-2),请用坐标表示出
所在的位置的坐标为(2,-2),请用坐标表示出 所在的位置(-3,2).
所在的位置(-3,2).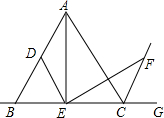 如图,△ABC是等边三角形,∠AEF=60°,ED∥AC交AB于点D,EF,交等边三角形外角平分线CF所在的直线与点F,当点E是BC的中点时,求证:AE=EF.
如图,△ABC是等边三角形,∠AEF=60°,ED∥AC交AB于点D,EF,交等边三角形外角平分线CF所在的直线与点F,当点E是BC的中点时,求证:AE=EF.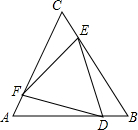 三边相等,三个角也相等的三角形叫做等边三角形,如图,△ABC和△DEF都是等边三角形,且D、E、F分别在AB、BC、CA边上.求证:AD=BE=CF.
三边相等,三个角也相等的三角形叫做等边三角形,如图,△ABC和△DEF都是等边三角形,且D、E、F分别在AB、BC、CA边上.求证:AD=BE=CF. (1)已知:如图,△ABC≌△A′B′C′,D是BC的中点,D′是B′C′的中点,求证:AD=A′D′;
(1)已知:如图,△ABC≌△A′B′C′,D是BC的中点,D′是B′C′的中点,求证:AD=A′D′;