题目内容
19.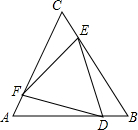 三边相等,三个角也相等的三角形叫做等边三角形,如图,△ABC和△DEF都是等边三角形,且D、E、F分别在AB、BC、CA边上.求证:AD=BE=CF.
三边相等,三个角也相等的三角形叫做等边三角形,如图,△ABC和△DEF都是等边三角形,且D、E、F分别在AB、BC、CA边上.求证:AD=BE=CF.
分析 由等边三角形的性质可知∠A=∠B=60°,DF=DE,且∠FDE=60°,所以可得出∠AFD=∠BDE,从而可证得△ADF≌△BED,同理可证得其它三角形全等,利用全等三角形的性质证得结论.
解答 证明:∵△ABC,△DEF是等边三角形,
∴∠A=∠B=60°,DF=DE,且∠FDE=60°,
∴∠BAD+∠ADF=∠ADF+∠AFD=120°,
∴∠AFD=∠BDE,
在△ADF和△BED中,
$\left\{\begin{array}{l}{∠A=∠B}\\{∠AFD=∠BDE}\\{DE=DF}\end{array}\right.$,
∴△ADF≌△BED(AAS),
同理可得:△ADF≌△CFE,
∴△ADF≌△CFE≌△BED;
∴AD=BE=CF.
点评 此题考查了等边三角形的判定与性质以及全等三角形的判定与性质.此题难度适中,熟练掌握全等三角形的判定和性质是解题的关键.

练习册系列答案
 小学教材全测系列答案
小学教材全测系列答案
相关题目
8.某商品经过两次连续提价,每件售价由原来的35元提到了55元.设平均每次提价的百分率为x,则下列方程中正确的是( )
| A. | 55 (1+x)2=35 | B. | 35(1+x)2=55 | C. | 55(1-x)2=35 | D. | 35(1-x)2=55 |
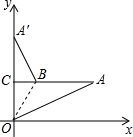 如图,Rt△AOC在平面直角坐标系中,OC在y轴上.OC=2,OA=5.将△AOC沿OB翻折使点A恰好落在y轴上的点A′的位置,则AB=$\frac{5\sqrt{21}}{7}$.
如图,Rt△AOC在平面直角坐标系中,OC在y轴上.OC=2,OA=5.将△AOC沿OB翻折使点A恰好落在y轴上的点A′的位置,则AB=$\frac{5\sqrt{21}}{7}$.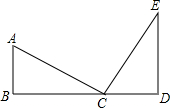 如图所示,点D为BC延长线上一点,点A,E是直线BC同侧的两点,∠B=90°,CD=AB,DE∥AB,AC⊥CE于C,求证:点C在线段AE的垂直平分线上.
如图所示,点D为BC延长线上一点,点A,E是直线BC同侧的两点,∠B=90°,CD=AB,DE∥AB,AC⊥CE于C,求证:点C在线段AE的垂直平分线上.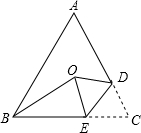 如图,在等腰△ABC中,AB=AC,将△ABC沿DE折叠,使底角顶点C落在三角形三边的垂直平分线的交点O处,若BE=BO,则∠ABC=63度.
如图,在等腰△ABC中,AB=AC,将△ABC沿DE折叠,使底角顶点C落在三角形三边的垂直平分线的交点O处,若BE=BO,则∠ABC=63度.