题目内容
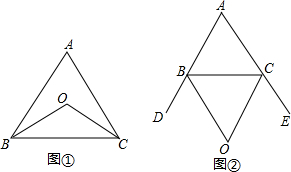
9.(1)如图1,三角形ABC中,BO平分∠ABC、CO平分∠ACB,则∠BOC与∠A的数量关系是∠BOC=90°+$\frac{1}{2}$∠A;(2)如图2,BO平分△ABC的外角∠CBD、CO平分△ABC的外角∠BCE,则∠BOC与∠A的关系是∠BOC=90°-$\frac{1}{2}$∠A;
(3)请就图2及图2中的结论进行证明.
分析 (1)根据角平分线的定义可得∠OBC=$\frac{1}{2}$∠ABC,∠OCB=$\frac{1}{2}$∠ACB,然后表示出∠OBC+∠OCB,再根据三角形的内角和等于180°列式整理即可;
(2)由三角形的一个外角等于与它不相邻的两个内角的和可证2∠1+2∠2=2∠A+∠ABC+∠ACB=∠A+180°,再根据三角形内角和定理可证2∠BOC=180°-∠A,即∠BOC=90°-$\frac{1}{2}$∠A;
(3)由三角形的一个外角等于与它不相邻的两个内角的和可证2∠1+2∠2=2∠A+∠ABC+∠ACB=∠A+180°,再根据三角形内角和定理可证2∠BOC=180°-∠A,即∠BOC=90°-$\frac{1}{2}$∠A.
解答 解:(1)∠BOC=90°+$\frac{1}{2}$∠A.
∵∠ABC与∠ACB的平分线相交于点O,
∴∠OBC=$\frac{1}{2}$∠ABC,∠OCB=$\frac{1}{2}$∠ACB,
∴∠OBC+∠OCB=$\frac{1}{2}$(∠ABC+∠ACB),
在△OBC中,∠BOC=180°-(∠OBC+∠OCB)
=180°-$\frac{1}{2}$(∠ABC+∠ACB)
=180°-$\frac{1}{2}$(180°-∠A)
=90°+$\frac{1}{2}$∠A,
故答案为:∠BOC=90°+$\frac{1}{2}$∠A;
(2)∠BOC与∠A的关系是∠BOC=90°-$\frac{1}{2}$∠A.
故答案为:∠BOC=90°-$\frac{1}{2}$∠A.
(3)证明:如图,
∵BO、CO分别是△ABC的外角∠DBC、∠ECB的角平分线,
∴∠DBC=2∠1=∠ACB+∠A,
∠ECB=2∠2=∠ABC+∠A,
∴2∠1+2∠2=2∠A+∠ABC+∠ACB=∠A+180°,
又∵∠1+∠2+∠BOC=180°,
∴2∠BOC=180°-∠A,
∴∠BOC=90°-$\frac{1}{2}$∠A.
点评 本题考查三角形外角的性质及三角形的内角和定理,解答的关键是沟通外角和内角的关系.


| A. | 100 | B. | 66 | C. | 36 | D. | 32 |
| A. | 垂直 | B. | 平行 | C. | 重合 | D. | 相交 |
 如图,△ABC中,∠C=90°,AC=3cm,点P是边BC上的动点,则AP长不可能是( )
如图,△ABC中,∠C=90°,AC=3cm,点P是边BC上的动点,则AP长不可能是( )| A. | 2.5cm | B. | 3cm | C. | 4cm | D. | 5cm |
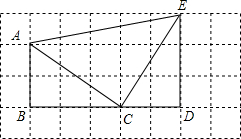 如图,若每个小方格边长为1,请你根据所学的知识判断△ACE是什么形状?并说明理由.
如图,若每个小方格边长为1,请你根据所学的知识判断△ACE是什么形状?并说明理由.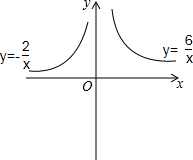 如图,在平面直角坐标系中,动点A从原点O出发沿y轴正半轴以每秒1单位长度运动,运动的时间为t秒,过点A作x轴的平行线,交函数y=-$\frac{2}{x}$(x<0)的图象于B,交函数y=$\frac{6}{x}$(x>0)的图象于C,作射线BO,点D是射线BO上一个动点.
如图,在平面直角坐标系中,动点A从原点O出发沿y轴正半轴以每秒1单位长度运动,运动的时间为t秒,过点A作x轴的平行线,交函数y=-$\frac{2}{x}$(x<0)的图象于B,交函数y=$\frac{6}{x}$(x>0)的图象于C,作射线BO,点D是射线BO上一个动点.