题目内容
9.在初中数学中,我们学习了“两点间的距离”、“点到直线的距离”、“平行线之间的距离”,距离的本质是“最短”,图形之间的距离总可以转化为两点之间的距离,如“垂线段最短”的性质,把点到直线的距离转化为点到点(垂足)的距离.一般的,一个图形上的任意点A与另一个图形上的任意点B之间的距离的最小值叫做两个图形的距离.
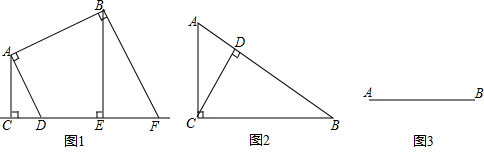
(1)如图1,过A,B分别作垂线段AC、AD、BE、BF,则线段AB和直线l的距离为垂线段AC的长度.
(2)如图2,Rt△ABC中,∠ACB=90°,∠B=30°,CD⊥AB,AD=2,那么线段AD与线段BC的距离为3.
(3)如图3,若长为1cm的线段CD与已知线段AB的距离为1.5cm,请用适当的方法表示满足条件的所有线段CD.
注:若满足条件的线段是有限的,请画出;若满足条件的线段是无限的,请用阴影表示其所在区域.(保留画图痕迹)
分析 (1)根据两图形之间距离定义,得出线段AB和直线l的距离即可;
(2)首先过点D作DE⊥BC于点E,进而利用直角三角形中30°所对的边等于斜边的一半,进而求出DE的长;
(3)根据两图形之间距离定义,利用CD的长为1cm,且线段CD与已知线段AB的距离为1.5cm,得出符合题意的图形是两个半圆以及矩形组成的图形.
解答  解:(1)如图所示:过A,B分别作垂线段AC、AD、BE、BF,
解:(1)如图所示:过A,B分别作垂线段AC、AD、BE、BF,
则线段AB和直线l的距离为垂线段为:AC的长度;
故答案为:AC;
(2)如图2,过点D作DE⊥BC于点E,
∵∠ACB=90°,∠B=30°,CD⊥AB,AD=2,
∴∠A=60°则∠ACD=30°,
∴AC=2AD=4,
∴AB=2AC=8,
∴BD=6,
则DE=$\frac{1}{2}$BD=3;
故答案为:3;
(3)如图3所示: .
.
点评 此题主要考查了应用设计与作图以及新定义,根据题意争正确把握两图形之间距离定义是解题关键.

练习册系列答案
 走进文言文系列答案
走进文言文系列答案
相关题目
15. 如图所示的几何体为圆台,其俯视图正确的是( )
如图所示的几何体为圆台,其俯视图正确的是( )
 如图所示的几何体为圆台,其俯视图正确的是( )
如图所示的几何体为圆台,其俯视图正确的是( )| A. |  | B. |  | C. |  | D. |  |
13.下列说法正确的是( )
| A. | |-2|=-2 | B. | 0的倒数是0 | C. | 4的平方根是2 | D. | -3的相反数是3 |
4.小王利用计算机设计了一个程序,输入和输出的数据如下表:
那么,当输入数据8时,输出的数据是( )
| 输入 | … | 1 | 2 | 3 | 4 | 5 | … |
| 输出 | … | $\frac{1}{2}$ | $\frac{2}{5}$ | $\frac{3}{10}$ | $\frac{4}{17}$ | $\frac{5}{26}$ | … |
| A. | $\frac{8}{61}$ | B. | $\frac{8}{63}$ | C. | $\frac{8}{65}$ | D. | $\frac{8}{67}$ |
18.如图,是某卖场国产大米牌手机的宣传广告.

(1)你认为大米手机5月份的销售量必定是三个品牌手机中最高的吗?通过计算说明你的理由.
(2)若各品牌手机2015年4月的销售量如下:
求该卖场5月份三个品牌手机销售量的平均增长率.

(1)你认为大米手机5月份的销售量必定是三个品牌手机中最高的吗?通过计算说明你的理由.
(2)若各品牌手机2015年4月的销售量如下:
| 手机品牌 | 芒果手机 | 四星手机 | 大米手机 |
| 销售量(台) | 200 | 80 | 120 |
 在边长为1的小正方形网格中,△AOB的顶点均在格点上,
在边长为1的小正方形网格中,△AOB的顶点均在格点上, 如图,在平面直角坐标系中,△ABC三个顶点分别为A(-1,4)、B(-3,1)、C(-3,4),△A1B1C1是由△ABC绕某一点顺时针旋转得到的.
如图,在平面直角坐标系中,△ABC三个顶点分别为A(-1,4)、B(-3,1)、C(-3,4),△A1B1C1是由△ABC绕某一点顺时针旋转得到的.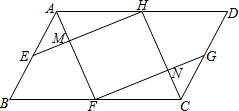 如图,在?ABCD中,E、F、G、H分别为AB、BC、CD、AD的中点,AF与EH交于点M,FG与CH交于点N.
如图,在?ABCD中,E、F、G、H分别为AB、BC、CD、AD的中点,AF与EH交于点M,FG与CH交于点N.