题目内容
1．如果实数x，y满足方程组$\left\{\begin{array}{l}{x+3y=0}\\{2x+3y=3}\end{array}\right.$，那么代数式（$\frac{xy}{x+y}$+2）÷$\frac{2}{x+y}$的值为$\frac{1}{2}$．分析 先根据分式混合运算的法则把原式进行化简，再求出x，y的值代入进行计算即可．
解答 解：原式=$\frac{2x+2y+xy}{x+y}$•$\frac{x+y}{2}$
=$\frac{2x+2y+xy}{2}$，
解方程组$\left\{\begin{array}{l}{x+3y=0}\\{2x+3y=3}\end{array}\right.$得，$\left\{\begin{array}{l}x=3\\ y=-1\end{array}\right.$，
故原式=$\frac{6-2-3}{2}$=$\frac{1}{2}$．
故答案为：$\frac{1}{2}$．
点评 本题考查的是分式的化简求值，熟知分式混合运算的法则是解答此题的关键．
练习册系列答案
作业辅导系列答案
同步学典一课多练系列答案
经典密卷系列答案
金牌课堂练系列答案
相关题目
11．杭州市汽车保有量统计，2015年私人汽车30.39万辆．为了缓解交通压力，整治雾霾，杭州已经开始限牌政策．把30.39万用科学记数法表示（ ）
| A． | 3.039×101 | B． | 3.039×104 | C． | 3.039×105 | D． | 30.39×104 |
12．描点法是研究函数图象的重要方法．那么对函数y=-x-$\frac{1}{x}$，你如果采用描点法的话，能得到该函数的正确性质是（ ）
| A． | 该函数图象与x轴相交 | B． | 该函数图象与y轴相交 | ||
| C． | 该函数图象关于原点成中心对称 | D． | 该函数图象是轴对称图形 |
16．使代数式$\frac{3}{2x-3}$有意义的x的取值范围是（ ）
| A． | x＜$\frac{3}{2}$ | B． | x=$\frac{3}{2}$ | C． | x＞$\frac{3}{2}$ | D． | x≠$\frac{3}{2}$ |
13．$\sqrt{（\sqrt{2015}-50）^{2}}$的值等于（ ）
| A． | ±（$\sqrt{2015}$-50） | B． | $\sqrt{2015}$±50 | C． | $\sqrt{2015}$-50 | D． | 50-$\sqrt{2015}$ |
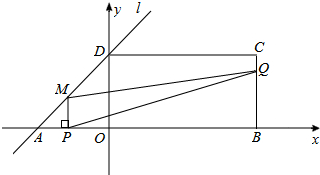如图，在平面直角坐标系中，四边形ABCD是一个面积为48的直角梯形，∠C=90°，∠DAO=45°，AB∥CD，点B（10，0）直线l经过点A，D两点，且动点P在线段AB上从点A出发以每秒2个单位的速度向点B运动，同时动点Q从点B出发以每秒4个单位的速度沿B→C→D的方向向点D运动，过点P作PM垂直于x轴，与折线A→D→C相交于点M，当P、Q两点中有一点到达终点时，另一点也随之停止运动，设点P，Q运动的时间为t秒（t＞0），△MPQ的面积为S．