题目内容
2.已知实数x,y满足$\sqrt{2x+y-5}$+x2+4y2=4xy,则(y-x)2015的值为( )| A. | 0 | B. | -1 | C. | 1 | D. | 2 015 |
分析 移项后根据完全平方公式变形,根据算术平方根和偶次方的非负性得出方程组,求出方程组的解,最后代入求出即可.
解答 解:∵$\sqrt{2x+y-5}$+x2+4y2=4xy,
∴$\sqrt{2x+y-5}$+x2+4y2-4xy=0,
∴$\sqrt{2x+y-5}$+(x-2y)2=0,
∴$\left\{\begin{array}{l}{2x+y-5=0}\\{x-2y=0}\end{array}\right.$,
解得:x=2,y=1,
∴(y-x)2015=(1-2)2015=-1,
故选B.
点评 本题考查了完全平方公式,算术平方根,二元一次方程组,求代数式的值的应用,解此题的关键是能得出关于x、y的方程组,题目比较典型,难度适中.

练习册系列答案
相关题目
12.描点法是研究函数图象的重要方法.那么对函数y=-x-$\frac{1}{x}$,你如果采用描点法的话,能得到该函数的正确性质是( )
| A. | 该函数图象与x轴相交 | B. | 该函数图象与y轴相交 | ||
| C. | 该函数图象关于原点成中心对称 | D. | 该函数图象是轴对称图形 |
13.$\sqrt{(\sqrt{2015}-50)^{2}}$的值等于( )
| A. | ±($\sqrt{2015}$-50) | B. | $\sqrt{2015}$±50 | C. | $\sqrt{2015}$-50 | D. | 50-$\sqrt{2015}$ |
7.在一个三角形中,已知AB=AC=6cm,BC=8cm,D是BC的中点,以D为圆心作一个半径为5cm的圆,则下列说法正确的是( )
| A. | 点A在⊙D外 | B. | 点B在⊙D上 | C. | 点C在⊙D内 | D. | 无法确定 |
3.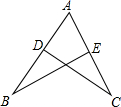 如图,AB=AC,若要使△ABE≌△ACD,则添加的一个条件不能是( )
如图,AB=AC,若要使△ABE≌△ACD,则添加的一个条件不能是( )
 如图,AB=AC,若要使△ABE≌△ACD,则添加的一个条件不能是( )
如图,AB=AC,若要使△ABE≌△ACD,则添加的一个条件不能是( )| A. | ∠B=∠C | B. | BE=CD | C. | BD=CE | D. | ∠ADC=∠AEB |
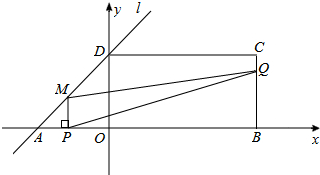 如图,在平面直角坐标系中,四边形ABCD是一个面积为48的直角梯形,∠C=90°,∠DAO=45°,AB∥CD,点B(10,0)直线l经过点A,D两点,且动点P在线段AB上从点A出发以每秒2个单位的速度向点B运动,同时动点Q从点B出发以每秒4个单位的速度沿B→C→D的方向向点D运动,过点P作PM垂直于x轴,与折线A→D→C相交于点M,当P、Q两点中有一点到达终点时,另一点也随之停止运动,设点P,Q运动的时间为t秒(t>0),△MPQ的面积为S.
如图,在平面直角坐标系中,四边形ABCD是一个面积为48的直角梯形,∠C=90°,∠DAO=45°,AB∥CD,点B(10,0)直线l经过点A,D两点,且动点P在线段AB上从点A出发以每秒2个单位的速度向点B运动,同时动点Q从点B出发以每秒4个单位的速度沿B→C→D的方向向点D运动,过点P作PM垂直于x轴,与折线A→D→C相交于点M,当P、Q两点中有一点到达终点时,另一点也随之停止运动,设点P,Q运动的时间为t秒(t>0),△MPQ的面积为S.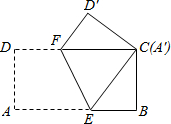 如图,将长为12cm,宽6cm的矩形纸片ABCD折叠,使点A与点C重合,则折痕EF的长为3$\sqrt{5}$cm.
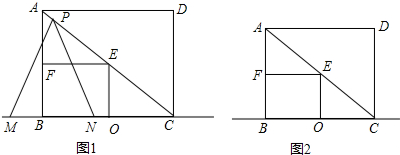
如图,将长为12cm,宽6cm的矩形纸片ABCD折叠,使点A与点C重合,则折痕EF的长为3$\sqrt{5}$cm.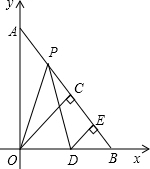 在△ABO中,∠AOB=90°,OA=OB=10,分别以边OA、OB所在的直线为坐标轴建立平面直角坐标系,点P自点A出发沿线段AB匀速运动至点B停止.同时点D自原点O出发沿x轴正方向匀速运动.在点P、D运动的过程中,始终满足PO=PD,过点O、D向直线AB做垂线,垂足分别为点C、E,设OD=x.
在△ABO中,∠AOB=90°,OA=OB=10,分别以边OA、OB所在的直线为坐标轴建立平面直角坐标系,点P自点A出发沿线段AB匀速运动至点B停止.同时点D自原点O出发沿x轴正方向匀速运动.在点P、D运动的过程中,始终满足PO=PD,过点O、D向直线AB做垂线,垂足分别为点C、E,设OD=x.