题目内容
3．已知a，b都是实数，且（12a+b）2+|3a-b-5|=0，求13a2-b的平方根．分析 根据已知等式利用非负数的性质求出a与b的值，代入原式计算求出平方根即可．
解答 解：∵（12a+b）2+|3a-b-5|=0，
∴$\left\{\begin{array}{l}{12a+b=0}\\{3a-b-5=0}\end{array}\right.$，
解得：$\left\{\begin{array}{l}{a=\frac{1}{3}}\\{b=-4}\end{array}\right.$，
∴原式=$\frac{49}{9}$，
则$\frac{49}{9}$的平方根是±$\frac{7}{3}$．
点评 此题考查了解二元一次方程组，平方根，以及非负数的性质，熟练掌握运算法则是解本题的关键．
练习册系列答案
一线名师提优试卷系列答案
相关题目
13．
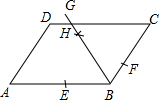如图，在?ABCD中，AB＞2BC，观察图中尺规作图的痕迹，则下列结论错误的是（ ）
如图，在?ABCD中，AB＞2BC，观察图中尺规作图的痕迹，则下列结论错误的是（ ）| A． | BG平分∠ABC | B． | BE=BF | C． | AD=CH | D． | CH=DH |
解不等式组：$\left\{\begin{array}{l}{2-3x≥2x-8}\\{\frac{2-x}{3}-2＜\frac{x-1}{2}}\end{array}\right.$，把它的解集在数轴上表示出来，并写出这个不等式组的整数解．
如图，在Rt△ABC中，∠ACB=90°，D、E、F分别是AB、BC、CA的中点，若CD=5cm，则EF=5cm．