题目内容
在平面直角坐标系xOy中,以原点O为圆心的圆过点A(-10,0),直线y=kx+3k-4与⊙O交于B、C两点,则弦BC的长的最小值为 .
考点:垂径定理,一次函数图象上点的坐标特征,勾股定理
专题:
分析:根据直线y=kx-3k+4必过点D(3,4),求出最短的弦CB是过点D且与该圆直径垂直的弦,再求出OD的长,再根据以原点O为圆心的圆过点A(-10,0),求出OB的长,再利用勾股定理求出BD,即可得出答案.
解答:解:∵直线y=kx-3k+4必过点D(3,4),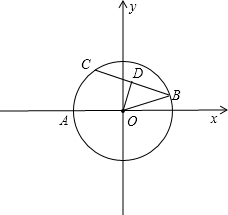
∴最短的弦CB是过点D且与该圆直径垂直的弦,
∵点D的坐标是(3,4),
∴OD=5,
∵以原点O为圆心的圆过点A(-10,0),
∴圆的半径为10,
∴OB=10,
∴BD=5
,
∴BC的长的最小值为10
;
故答案为:10
.

∴最短的弦CB是过点D且与该圆直径垂直的弦,
∵点D的坐标是(3,4),
∴OD=5,
∵以原点O为圆心的圆过点A(-10,0),
∴圆的半径为10,
∴OB=10,
∴BD=5
| 3 |
∴BC的长的最小值为10
| 3 |
故答案为:10
| 3 |
点评:此题考查了一次函数的综合,用到的知识点是垂径定理、勾股定理、圆的有关性质,关键是求出BC最短时的位置.

练习册系列答案
相关题目
下列各组数可能构成一个三角形的是( )
| A、2,2,4 |
| B、3,5,9 |
| C、4,7,8 |
| D、5,5,11 |
 在菱形ABCD中,下列结论一定正确的是( )
在菱形ABCD中,下列结论一定正确的是( )| A、AD=BD |
| B、菱形ABCD的面积是AC和BD的积 |
| C、∠DAC=∠BAC |
| D、∠ACB=30° |


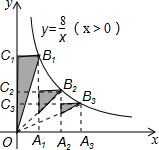 如图,A1、A2、A3…An在x轴上,且OA1=A1A2=A2A3=…=An-1An,分别过点A1、A2、A3…An作y轴的平行线,与反比例函数y=
如图,A1、A2、A3…An在x轴上,且OA1=A1A2=A2A3=…=An-1An,分别过点A1、A2、A3…An作y轴的平行线,与反比例函数y=