题目内容
如图1,两个直角三角形拼成一个四边形ABCD,其中∠B=∠D=90°,AD=BC.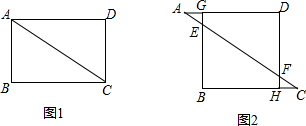
(1)求证:四边形ABCD是矩形;
(2)△ABC不动,△ADC沿CA方向平移,重新标注字母后如图2,割掉Rt△AEG和Rt△CFH后,得到一个正方形DGBH,若AD=18,DF=12,求正方形DGBH的边长.

(1)求证:四边形ABCD是矩形;
(2)△ABC不动,△ADC沿CA方向平移,重新标注字母后如图2,割掉Rt△AEG和Rt△CFH后,得到一个正方形DGBH,若AD=18,DF=12,求正方形DGBH的边长.
考点:矩形的判定,全等三角形的判定与性质,正方形的性质,相似三角形的判定与性质
专题:
分析:(1)首先利用HL证得Rt△ABC≌Rt△CDA,从而得到∠ACB=∠CAD,进一步得到AD∥BC,从而判定四边形ABCD是平行四边形,证得四边形ABCD为矩形;
(2)设DG=BG=x,根据GE∥DF,得到△AGE∽△ADF,从而列出有关x的方程求得x的值即可.
(2)设DG=BG=x,根据GE∥DF,得到△AGE∽△ADF,从而列出有关x的方程求得x的值即可.
解答:(1)证明:∵在Rt△ABC和Rt△CDA中,
∴Rt△ABC≌Rt△CDA,
∴∠ACB=∠CAD,
∴AD∥BC,
∵AD=BC,
∴四边形ABCD是平行四边形,
∴四边形ABCD为矩形;
(2)解:设DG=BG=x,
∵GE∥DF,
∴△AGE∽△ADF,
∴
=
,
即:
=
,
解得:x=
.
答:正方形DGBH的边长
.
|
∴Rt△ABC≌Rt△CDA,
∴∠ACB=∠CAD,
∴AD∥BC,
∵AD=BC,
∴四边形ABCD是平行四边形,
∴四边形ABCD为矩形;
(2)解:设DG=BG=x,
∵GE∥DF,
∴△AGE∽△ADF,
∴
| AG |
| AD |
| GE |
| DF |
即:
| 18-x |
| 18 |
| x-12 |
| 12 |
解得:x=
| 72 |
| 5 |
答:正方形DGBH的边长
| 72 |
| 5 |
点评:本题考查了矩形的判定,题目中还渗透了方程的数学思想,解题的关键是了解矩形的判定方法,难度中等.

练习册系列答案
相关题目
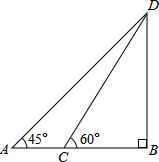 某校数学兴趣小组测量一座大桥高度,如图所示,他们在A处测得大桥最高点D的仰角为45°,在前方240m的C处测得大桥最高点D的仰角为60°,求该兴趣小组测得的大桥高度DB.(
某校数学兴趣小组测量一座大桥高度,如图所示,他们在A处测得大桥最高点D的仰角为45°,在前方240m的C处测得大桥最高点D的仰角为60°,求该兴趣小组测得的大桥高度DB.(
