题目内容
 在已建立直角坐标系的4×4正方形方格纸中,若每个小正方形的边长为1,在4×4方格纸中平移一次线段BC后的像为AD,以A,B,C,D为顶点的四边形是菱形,
在已建立直角坐标系的4×4正方形方格纸中,若每个小正方形的边长为1,在4×4方格纸中平移一次线段BC后的像为AD,以A,B,C,D为顶点的四边形是菱形,(1)求线段AD所在的直线解析式;
(2)线段BC扫过的面积.
考点:作图-平移变换,待定系数法求一次函数解析式,菱形的性质
专题:
分析:(1)根据菱形的性质以及待定系数法求一次函数解析式方法分别求出即可;
(2)利用勾股定理以及菱形的面积公式求出即可.
(2)利用勾股定理以及菱形的面积公式求出即可.
解答: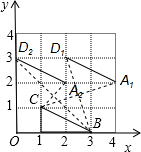 解:(1)由题意可得,平移后的像的坐标如图A1(4,2),D1(2,3),或A2(2,2),D2(0,3)
解:(1)由题意可得,平移后的像的坐标如图A1(4,2),D1(2,3),或A2(2,2),D2(0,3)
设AD所在的直线解析式y=kx+b(k≠0)
把A1(4,2),D1(2,3)代入
解得
∴y=-
x+4,
同理把A2(2,2),D2(0,3)代入解得另一解析式为:
∴y=-
x+3;
(2)线段BC扫过的面积为:S菱形CBA1D1=
×CA1×BD1=
×
×
=5,
S菱形CBA2D2=
×CA2×BD2=
×
×3
=3,
综上所述:线段BC扫过的面积为:3或5.
 解:(1)由题意可得,平移后的像的坐标如图A1(4,2),D1(2,3),或A2(2,2),D2(0,3)
解:(1)由题意可得,平移后的像的坐标如图A1(4,2),D1(2,3),或A2(2,2),D2(0,3)设AD所在的直线解析式y=kx+b(k≠0)
把A1(4,2),D1(2,3)代入
|
解得
|
∴y=-
| 1 |
| 2 |
同理把A2(2,2),D2(0,3)代入解得另一解析式为:
∴y=-
| 1 |
| 2 |
(2)线段BC扫过的面积为:S菱形CBA1D1=
| 1 |
| 2 |
| 1 |
| 2 |
| 10 |
| 10 |
S菱形CBA2D2=
| 1 |
| 2 |
| 1 |
| 2 |
| 2 |
| 2 |
综上所述:线段BC扫过的面积为:3或5.
点评:此题主要考查了利用平移设计图案以及菱形的性质和面积求法以及待定系数法求一次函数解析式等知识,得出平移后对应点坐标是解题关键.

练习册系列答案
 一线名师权威作业本系列答案
一线名师权威作业本系列答案
相关题目
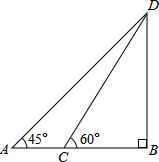 某校数学兴趣小组测量一座大桥高度,如图所示,他们在A处测得大桥最高点D的仰角为45°,在前方240m的C处测得大桥最高点D的仰角为60°,求该兴趣小组测得的大桥高度DB.(
某校数学兴趣小组测量一座大桥高度,如图所示,他们在A处测得大桥最高点D的仰角为45°,在前方240m的C处测得大桥最高点D的仰角为60°,求该兴趣小组测得的大桥高度DB.(
