题目内容
6.阅读下面的解答过程,然后作答:有这样一类题目:将$\sqrt{a+2\sqrt{b}}$化简,若你能找到两个数 m和n,使m2+n2=a 且 mn=$\sqrt{b}$,则a+2$\sqrt{b}$ 可变为m2+n2+2mn,即变成(m+n)2,从而使得$\sqrt{a+2\sqrt{b}}$ 化简.
例如:∵5+2$\sqrt{6}$=3+2+2$\sqrt{6}$=($\sqrt{3}$)2+($\sqrt{2}$)2+2$\sqrt{6}$=($\sqrt{3}$+$\sqrt{2}$)2
∴$\sqrt{5+2\sqrt{6}}$=$\sqrt{(\sqrt{3}+\sqrt{2})^{2}}$=$\sqrt{3}$+$\sqrt{2}$
请你仿照上例解下面问题(1)$\sqrt{4+2\sqrt{3}}$(2)$\sqrt{7-2\sqrt{10}}$.
分析 (1)利用完全平方公式把4+2$\sqrt{3}$化为(1+$\sqrt{3}$)2,然后利用二次根式的性质化简即可.
(2)利用完全平方公式把7-2$\sqrt{10}$化为($\sqrt{5}$-$\sqrt{2}$)2然后利用二次根式的性质化简即可.
解答 解:(1)∵4+2$\sqrt{3}$=1+3+2$\sqrt{3}$=12+$(\sqrt{3})^{2}$+2$\sqrt{3}$=(1+$\sqrt{3}$)2,
∴$\sqrt{4+2\sqrt{3}}$=$\sqrt{(1+\sqrt{3})^{2}}$=1+$\sqrt{3}$;
(2)$\sqrt{7-2\sqrt{10}}$=$\sqrt{(\sqrt{5})^{2}+(\sqrt{2})^{2}-2×\sqrt{5}×\sqrt{2}}$=$\sqrt{(\sqrt{5}-\sqrt{2})^{2}}$=$\sqrt{5}$-$\sqrt{2}$.
点评 本题主要考查了二次根式的性质与化简,解题的关键是熟记掌握完全平方公式.

练习册系列答案
相关题目
11.下列各式计算正确的是( )
| A. | 6x6÷2x2=3x2 | B. | 8x8÷4x2=2x6 | C. | a3÷a3=0 | D. | $\frac{2}{3}$a5b÷$\frac{3}{2}$a5b=1 |
16.若x-y>x,且x+y<y,则下列不等式中正确的是( )
| A. | xy<0 | B. | $\frac{x}{y}$>0 | C. | x+y>0 | D. | x-y<0 |
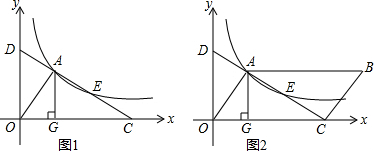
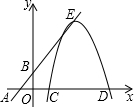 如图,一次函数y=x+2与x轴交于点A,与y轴交于点B,一抛物线的顶点在直线AB上,形状与函数y=-$\frac{1}{2}$x2图象相同,它与x轴分别交于点C、D(点C在点D的左侧),抛物线的顶点为点E.
如图,一次函数y=x+2与x轴交于点A,与y轴交于点B,一抛物线的顶点在直线AB上,形状与函数y=-$\frac{1}{2}$x2图象相同,它与x轴分别交于点C、D(点C在点D的左侧),抛物线的顶点为点E.
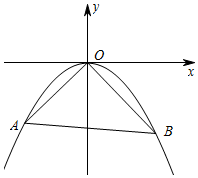 如图,直线y=kx+b(b<0)与抛物线y=ax2相交于点A(x1,y1),B(x2,y2)两点,抛物线y=ax2经过点(4,-2)
如图,直线y=kx+b(b<0)与抛物线y=ax2相交于点A(x1,y1),B(x2,y2)两点,抛物线y=ax2经过点(4,-2)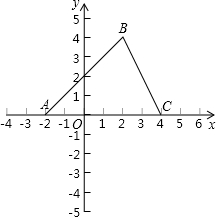 如图,在直角坐标系中,△ABC的顶点A(-2,0),B(2,4),C(4,0).
如图,在直角坐标系中,△ABC的顶点A(-2,0),B(2,4),C(4,0).