题目内容
13.如图1,已知在长方形ABCD中,AD=8,AB=4,将长方形ABCD沿着对角线BD折叠,使点C落在C'处,BC'交AD于点E.(1)求证:△BED是等腰三角形.
(2)求DE的长.
(3)如图2,若点P是BD上一动点,PN⊥BE于点N,PM⊥AD于点M,问:PN+PM的长是否为定值?如果是,请求出该值,如果不是,请说明理由.
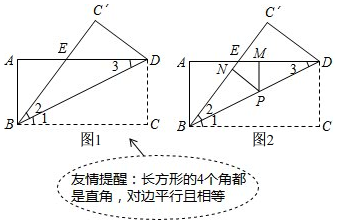
分析 (1)由折叠和平行线性质可得:∠3=∠2,根据等角对等边得BE=DE,所以△BDE是等腰三角形;
(2)设DE=x,则AE=8-x,BE=x,根据勾股定理列方程可求得AE的长;
(3)先判断出PH⊥BC,再用角平分线定理得出PN=PH,即可得出结论.
解答 解:(1)由翻折知,∠1=∠2,
∵AD∥BC,
∴∠3=∠2,
∴∠1=∠3,
∴BE=DE,
即△BED是等腰三角形;
(2)设DE=x,则AE=8-x,BE=x,
在Rt△ABE中,x2=(8-x)2+42,
解之,x=5,
∴DE=5;
(3)PM+PN为定值,是4,
如图,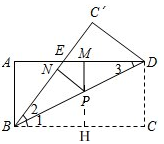
延长MP,交BC于点H,
∵AD∥BC,PM⊥AD,
∴PH⊥BC,
∵∠1=∠2,PN⊥BE,PH⊥BC,
∴PN=PH,
∴PM+PN=MN=AB=4.
点评 此题是四边形综合题,主要考查了矩形、折叠的性质及等腰三角形的判定、勾股定理,角平分线定理,在四边形计算中,常利用勾股定理列方程求边的长度.

练习册系列答案
 各地期末复习特训卷系列答案
各地期末复习特训卷系列答案 小博士期末闯关100分系列答案
小博士期末闯关100分系列答案
相关题目

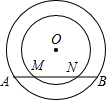 如图,同心⊙O中,大圆弦AB与小圆交于点M、N.
如图,同心⊙O中,大圆弦AB与小圆交于点M、N.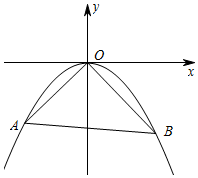 如图,直线y=kx+b(b<0)与抛物线y=ax2相交于点A(x1,y1),B(x2,y2)两点,抛物线y=ax2经过点(4,-2)
如图,直线y=kx+b(b<0)与抛物线y=ax2相交于点A(x1,y1),B(x2,y2)两点,抛物线y=ax2经过点(4,-2)
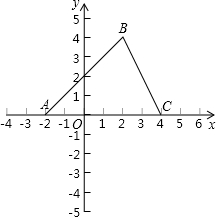 如图,在直角坐标系中,△ABC的顶点A(-2,0),B(2,4),C(4,0).
如图,在直角坐标系中,△ABC的顶点A(-2,0),B(2,4),C(4,0).