题目内容
20.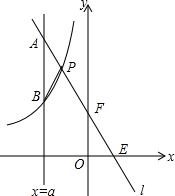 如图,一次函数y=kx+b的图象l与坐标轴分别交于点E、F,与双曲线y=-$\frac{2}{x}$(x<0)交于点P(-1,n),且F是PE的中点.
如图,一次函数y=kx+b的图象l与坐标轴分别交于点E、F,与双曲线y=-$\frac{2}{x}$(x<0)交于点P(-1,n),且F是PE的中点.(1)求直线l的解析式;
(2)若直线x=a与l交于点A,与双曲线交于点B(不同于A),问a为何值时,PA=PB?
分析 (1)先由y=-$\frac{2}{x}$(x<0),求出点P的坐标,再根据F为PE中点,求出F的坐标,把P,F的坐标代入求出直线l的解析式;
(2)过P作PD⊥AB,垂足为点D,由A点的纵坐标为-a+1,B点的纵坐标为-$\frac{2}{a}$,D点的纵坐标为2,列出方程求解即可.
解答 解:(1)∵双曲线y=-$\frac{2}{x}$(x<0)经过点P(-1,n),
∴n=-$\frac{2}{-1}$=2,
∴P(-1,2),
∵F是PE的中点,
∴OF=$\frac{1}{2}$×2=1,
∴F(0,1),
设直线l的解析式为y=kx+b,
∴$\left\{\begin{array}{l}{-k+b=2}\\{b=1}\end{array}\right.$,解得$\left\{\begin{array}{l}{k=-1}\\{b=1}\end{array}\right.$,
∴直线l的解析式为y=-x+1;
(2)如图,过P作PD⊥AB,垂足为点D,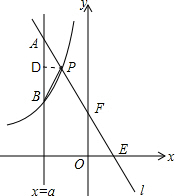
∵PA=PB,
∴点D为AB的中点,
又由题意知A点的纵坐标为-a+1,B点的纵坐标为-$\frac{2}{a}$,D点的纵坐标为2,
∴得方程-a+1-$\frac{2}{a}$=2×2,
解得a1=-2,a2=-1(舍去).
∴当a=-2时,PA=PB.
点评 本题主要考查了反比例函数与一次函数的交点,解题的重点是求出直线l的解析式.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
15.某水果市场上的苹果的价格如下:
甲、乙两组共买了100kg苹果,甲组比乙组少花38元,问甲组比乙组少买多少苹果?
| 购买苹果数量 | 不超过30千克 | 超30千克但不超过50千克 | 50千克以上 |
| 每千克价格/元 | 3元 | 2.5元 | 2元 |
5.下列计算正确的是( )
| A. | 2a-a=1 | B. | a2+a2=2a4 | C. | a2•a3=a5 | D. | (a-b)2=a2-b2 |
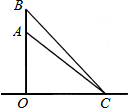 如图,一只松鼠在树干的A处,从地面C测得AC的距离是6m,仰角是43°,1s后,松鼠跳到B处,此时测得BC的距离是6.13m,仰角为45.54°,解答下列问题
如图,一只松鼠在树干的A处,从地面C测得AC的距离是6m,仰角是43°,1s后,松鼠跳到B处,此时测得BC的距离是6.13m,仰角为45.54°,解答下列问题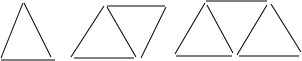 用牙签按下图的方式搭三角形,搭n个这样的三角形需要2n+1根牙签.
用牙签按下图的方式搭三角形,搭n个这样的三角形需要2n+1根牙签.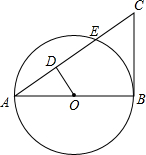 如图,AB为⊙O的直径,BC为⊙O的切线,AC交⊙O于点E,D为AC上一点,∠AOD=∠C.
如图,AB为⊙O的直径,BC为⊙O的切线,AC交⊙O于点E,D为AC上一点,∠AOD=∠C.