题目内容
10.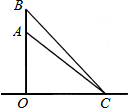 如图,一只松鼠在树干的A处,从地面C测得AC的距离是6m,仰角是43°,1s后,松鼠跳到B处,此时测得BC的距离是6.13m,仰角为45.54°,解答下列问题
如图,一只松鼠在树干的A处,从地面C测得AC的距离是6m,仰角是43°,1s后,松鼠跳到B处,此时测得BC的距离是6.13m,仰角为45.54°,解答下列问题(1)B点距离地面有多远(精确到0.01m)
(2)松鼠从A点跳到B点的平均速度是多少(精确到0.1m/s)
(参考数据:sin45.54°≈0.714,sin43°≈0.682,tan43°≈0.933)
分析 (1)在Rt△BOC中,根据$\frac{BO}{BC}$=sin∠BCO,求出BO的长即可;
(2)在Rt△AOC中,根据$\frac{AO}{AC}$=sin∠ACO,求出AO的长,然后根据AB=BO-AO,求出AB的长,从而可知A点跳到B点的平均速度.
解答 解:(1)在Rt△BOC中,$\frac{BO}{BC}$=sin∠BCO,
即$\frac{BO}{6.13}$=sin45.54°,
解得,BO≈0.714×6.13≈4.38米.
(2)在Rt△AOC中,$\frac{AO}{AC}$=sin∠ACO,
即$\frac{AO}{AC}$=sin43°,
$\frac{AO}{6}$=0.682,
解得,AO≈6×0.682≈4.092米,
AB=BO-AO=4.38-4.092=0.288米,
松鼠从A点跳到B点的平均速度是0.288÷1≈0.29米.
点评 本题考查了解直角三角形的应用--仰角俯角问题,要求学生能借助仰角构造直角三角形并解直角三角形.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
1.某文具店为了了解2015年3月份计算器的销售情况,对该月各种型号计算器的情况进行了统计,并将统计的结果绘制成如下两幅不完整的统计图.
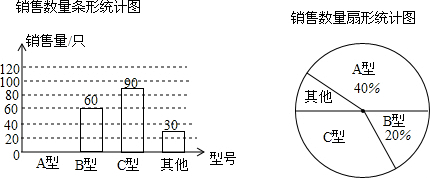
(1)请根据图中提供的信息,将条形图补充完整.
(2)该店4月份只购进了A,B,C三种型号的计算器,其数量和与3份计算器销量的总数量相同,结果恰好用完进化款共8200元,设购进A型计算器x只,B型计算器y只,三种计算器的进价和售价如下表:
求出y与x之间的函数关系式.
(3)在(2)中的条件下,根据实际情况,预计B型计算器销售超过40只后,这种型号的计算器就会产生滞销.
①假设所购进的A,B,C三种型号计算器能全部售出,求出预估利润P(元)与x(只)的函数关系式;
②求出预估利润的最大值.

(1)请根据图中提供的信息,将条形图补充完整.
(2)该店4月份只购进了A,B,C三种型号的计算器,其数量和与3份计算器销量的总数量相同,结果恰好用完进化款共8200元,设购进A型计算器x只,B型计算器y只,三种计算器的进价和售价如下表:
| A型 | B型 | C型 | |
| 进价(元/只) | 50 | 30 | 20 |
| 售价(元/只) | 70 | 45 | 25 |
(3)在(2)中的条件下,根据实际情况,预计B型计算器销售超过40只后,这种型号的计算器就会产生滞销.
①假设所购进的A,B,C三种型号计算器能全部售出,求出预估利润P(元)与x(只)的函数关系式;
②求出预估利润的最大值.
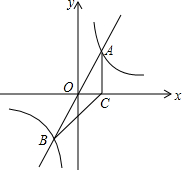 如图,直线y=mx与双曲线y=$\frac{k}{x}$相交于A、B两点,A点的坐标为(1,2),AC⊥x轴于C,连结BC.
如图,直线y=mx与双曲线y=$\frac{k}{x}$相交于A、B两点,A点的坐标为(1,2),AC⊥x轴于C,连结BC.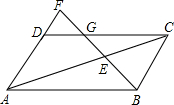 如图,?ABCD的边AD的延长线上取一点F,BF分别交AC,DC于点E,G,且EF=32cm,GF=18cm,求BE的长.
如图,?ABCD的边AD的延长线上取一点F,BF分别交AC,DC于点E,G,且EF=32cm,GF=18cm,求BE的长.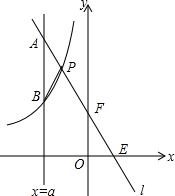 如图,一次函数y=kx+b的图象l与坐标轴分别交于点E、F,与双曲线y=-$\frac{2}{x}$(x<0)交于点P(-1,n),且F是PE的中点.
如图,一次函数y=kx+b的图象l与坐标轴分别交于点E、F,与双曲线y=-$\frac{2}{x}$(x<0)交于点P(-1,n),且F是PE的中点.