题目内容
 如图所示,在?ABCD中,AC与BD交于点O,EG⊥FH于点O.求证:四边形EFGH为菱形.
如图所示,在?ABCD中,AC与BD交于点O,EG⊥FH于点O.求证:四边形EFGH为菱形.考点:菱形的判定,平行四边形的性质
专题:证明题
分析:根据对角线互相垂直的平行四边形是菱形.由已知条件证明OH=OF,同理OE=OG,所以四边形EFGH是平行四边形,又因为EG⊥FH,所以四边形EFGH是菱形.
解答:证明:∵在平行四边形ABCD中,OD=OB,OA=OC,AD∥CB,
∴∠HAO=∠FCO,
在△AHO和△CFO中,
,
∴△AHO≌△CFO(ASA),
∴OH=OF
同理OE=OG,
∴四边形EFGH是平行四边形,
又∵EG⊥FH,
∴平行四边形EFGH是菱形
∴∠HAO=∠FCO,
在△AHO和△CFO中,
|
∴△AHO≌△CFO(ASA),
∴OH=OF
同理OE=OG,
∴四边形EFGH是平行四边形,
又∵EG⊥FH,
∴平行四边形EFGH是菱形
点评:本题考查了平行四边形的性质和判定,全等三角形的性质和判定,菱形的判定的应用,主要考查学生的推理能力.

练习册系列答案
 中考解读考点精练系列答案
中考解读考点精练系列答案
相关题目
 如图,在△CDE中,∠E=90°,DE=6,CD=10,求tanD+
如图,在△CDE中,∠E=90°,DE=6,CD=10,求tanD+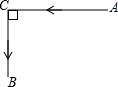 甲船和乙船分别从A港和C港同时出发,各沿图中箭头所指的方向航行(如图所示).现已知甲、乙两船的速度分别是16海里/时和12海里/时,且A,C两港之间的距离为10海里.问:经过多长时间,甲船和乙船之间的距离最短?最短距离为多少?(注:题中的“距离”都指直线距离,图中AC⊥CB.)
甲船和乙船分别从A港和C港同时出发,各沿图中箭头所指的方向航行(如图所示).现已知甲、乙两船的速度分别是16海里/时和12海里/时,且A,C两港之间的距离为10海里.问:经过多长时间,甲船和乙船之间的距离最短?最短距离为多少?(注:题中的“距离”都指直线距离,图中AC⊥CB.) 如图,一艘轮船按箭头所示方向行驶,C处有一灯塔,请根据图中所标数据求∠ACB的大小,并且求当轮船距离灯塔C最近时,∠ACB是多少度?
如图,一艘轮船按箭头所示方向行驶,C处有一灯塔,请根据图中所标数据求∠ACB的大小,并且求当轮船距离灯塔C最近时,∠ACB是多少度? 如图,移动其中两根火柴棒,使图形变成一个中心对称图形.
如图,移动其中两根火柴棒,使图形变成一个中心对称图形.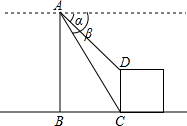 关于三角函数有如下的公式:sin(α+β)=sinαcosβ+cosαsinβ;
关于三角函数有如下的公式:sin(α+β)=sinαcosβ+cosαsinβ;