题目内容
如图，在△CDE中，∠E=90°，DE=6，CD=10，求tanD+| cosD |
| 1+sinD |
考点：解直角三角形
专题：
分析：首先根据勾股定理求得CE的长度，然后根据锐角三角函数的定义进行解答．
解答：解：如图，∵在△CDE中，∠E=90°，DE=6，CD=10，
∴由勾股定理，得
CE=
=
=8．
则tanD=
=
=
，cosD=
=
=
，sinD=
=
=
．
∴tanD+
=
+
=
，即tanD+
的值是
．
∴由勾股定理，得
CE=
| CD2-ED2 |
| 102-62 |
则tanD=
| CE |
| ED |
| 8 |
| 6 |
| 4 |
| 3 |
| ED |
| CD |
| 6 |
| 10 |
| 3 |
| 5 |
| EC |
| CD |
| 8 |
| 10 |
| 4 |
| 5 |
∴tanD+
| cosD |
| 1+sinD |
| 4 |
| 3 |
| ||
1+
|
| 5 |
| 3 |
| cosD |
| 1+sinD |
| 5 |
| 3 |
点评：本题考查了解直角三角形．要熟练掌握好边角之间的关系．
练习册系列答案
阅读快车系列答案
相关题目
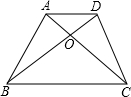如图，在梯形ABCD中，AD∥BC，对角线AC，BD相交于点O．若S△AOD：S△BOC=1：4，则S△AOD：S△ACD为（ ）| A、1：6 | B、1：5 |
| C、1：4 | D、1：3 |
下列命题中，正确的是（ ）
| A、三角形的外心是三角形三条高线的交点 |
| B、等腰三角形的外心一定在它的内部 |
| C、任何一个三角形有且仅有一个外接圆 |
| D、三角形的内心可能在它的外部 |
若两个图形成中心对称，则下列说法：
①对应点的连线必经过对称中心；
②这两个图形的形状和大小完全相同；
③这两个图形的对应线段一定相等；
④将一个图形绕对称中心旋转某个角度后必与另一个图形重合．
其中正确的有（ ）
①对应点的连线必经过对称中心；
②这两个图形的形状和大小完全相同；
③这两个图形的对应线段一定相等；
④将一个图形绕对称中心旋转某个角度后必与另一个图形重合．
其中正确的有（ ）
| A、1个 | B、2个 | C、3个 | D、4个 |
在反比例函数y=-
的图象上，坐标为整数的点的个数为（ ）
| 6 |
| x |
| A、4个 | B、6个 | C、8个 | D、10个 |
如图，AM=AN，BM=BN，求证：△AMB≌△ANB．
如图所示，在?ABCD中，AC与BD交于点O，EG⊥FH于点O．求证：四边形EFGH为菱形．