题目内容
 如图,将平行四边形ABCD纸片沿EF折叠,使点C与点A重合,点D落在点G处,
如图,将平行四边形ABCD纸片沿EF折叠,使点C与点A重合,点D落在点G处,(1)求证:AE=AF;
(2)求证:△ABE≌△AGF.
考点:翻折变换(折叠问题)
专题:证明题
分析:(1)根据折叠的性质可得∠CEF=∠AEF,根据平行线的性质可得∠CEF=∠EFA,根据等量关系可得∠AEF=∠EFA,根据等角对等边即可求解;
(2)根据平行四边形的性质,可得AB=CD,∠BAD=∠BCD,根据折叠的性质,可得AG=CD,∠EAG=∠BCD,所以AB=AG,∠BAD=∠EAG,由等量代换可得∠BAE=∠GAF,得到AB∥CD,AE∥GF,AD∥BC,得到∠BEA=∠EAF=∠GFA,AAS可证△ABE≌△AGF.
(2)根据平行四边形的性质,可得AB=CD,∠BAD=∠BCD,根据折叠的性质,可得AG=CD,∠EAG=∠BCD,所以AB=AG,∠BAD=∠EAG,由等量代换可得∠BAE=∠GAF,得到AB∥CD,AE∥GF,AD∥BC,得到∠BEA=∠EAF=∠GFA,AAS可证△ABE≌△AGF.
解答:(1)证明:由折叠的性质可得∠CEF=∠AEF,
∵四边形ABCD是平行四边形,
∴AD∥BC,
∴∠CEF=∠EFA,
∴∠AEF=∠EFA,
∴AE=AF;
(2)证明:∵四边形ABCD是平行四边形,
∴AB=CD,∠BAD=∠BCD,
又根据题意得:AG=CD,∠EAG=∠BCD,
∴AB=AG,∠BAD=∠EAG,
∴∠BAE=∠GAF,
又∵AB∥CD,AE∥GF,AD∥BC,
∴∠BEA=∠EAF=∠GFA,
在△ABE与△AGF中,
,
∴△ABE≌△AGF(AAS).
∵四边形ABCD是平行四边形,
∴AD∥BC,
∴∠CEF=∠EFA,
∴∠AEF=∠EFA,
∴AE=AF;
(2)证明:∵四边形ABCD是平行四边形,
∴AB=CD,∠BAD=∠BCD,
又根据题意得:AG=CD,∠EAG=∠BCD,
∴AB=AG,∠BAD=∠EAG,
∴∠BAE=∠GAF,
又∵AB∥CD,AE∥GF,AD∥BC,
∴∠BEA=∠EAF=∠GFA,
在△ABE与△AGF中,
|
∴△ABE≌△AGF(AAS).
点评:此题是折叠问题,是中考中的常见题目.解此题首先要注意折叠前后的部分全等,即对应角与对应边都相等.解此题还要注意平行四边形的性质的求解方法.

练习册系列答案
相关题目
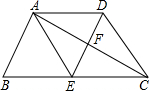 如图,在梯形ABCD中,AD∥BC,E为BC的中点,BC=2AD,EA=ED,AC与ED相交于点F.求证:梯形ABCD是等腰梯形.
如图,在梯形ABCD中,AD∥BC,E为BC的中点,BC=2AD,EA=ED,AC与ED相交于点F.求证:梯形ABCD是等腰梯形.
 如图,在平面直角坐标系中,已知A点坐标(4,0),B点坐标(0,8),点M是线段OA上一动点(不与点O、点A重合),点N是线段OB上一动点,且运动时始终保持ON=2AM,连接MN,并作△OMN的角平分线OD交线段MN于点D.
如图,在平面直角坐标系中,已知A点坐标(4,0),B点坐标(0,8),点M是线段OA上一动点(不与点O、点A重合),点N是线段OB上一动点,且运动时始终保持ON=2AM,连接MN,并作△OMN的角平分线OD交线段MN于点D.