题目内容
6.已知抛物线y=ax2+bx+c(a≠0)过点A(1,0)、B(3,0)、C(0,3),顶点为D.(1)求抛物线的解析式;
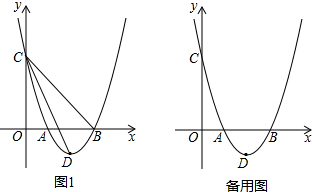
(2)判断△BCD与△AOC的关系,并说明理由;
(3)在抛物线y=ax2+bx+c上有一点G,使得∠GAB=∠BCD,直接写出符合条件的点G的坐标;
(※不计总分)设△ABD的外接圆为⊙E,直线l经过点B且垂直于x轴,点P是⊙E上异于A、B的任意一点,直线AP交l于点M,连接EM、PB.那么tan∠MEB•tan∠PBA的值为2.
分析 (1)直接将A(1,0)、B(3,0)、C(0,3)代入抛物线y=ax2+bx+c建立方程组,求出a、b、c的值就可以求出结论;
(2)如图1,过点G作GF⊥x轴,垂足为F.设点G坐标为(m,m2-4m+3),由抛物线的解析式就可以求出D的坐标,由勾股定理的逆定理就可以求出△BDC是直角三角形,再求出三角形各边长,计算出相似比就可以求出结论;
(3)如图2,①过点G作GF⊥x轴,垂足为F.设点G坐标为(m,m2-4m+3),利用tan∠GAF=tan∠BCD=$\frac{1}{3}$,得到-3(m2-4m+3)=m-1,求出m的值,进而求出G的坐标;②过点G1作G1F⊥x轴,垂足为F.设点G1坐标为(m,m2-4m+3),同①,求出G1坐标.
如图3,由条件可以求得△ADB为等腰直角三角形,就可以求出E的坐标.设P(x1,y1)(1<x1<3,y1≠0),M(3,y0),作PF⊥x轴,F为垂足.就可以得出△AFP∽△ABM,就可以表示出y0的值,由直角三角形的性质就可以表示出tan∠MEB和tan∠PBA的值,从而得出结论.
解答 解:(1)由抛物线y=ax2+bx+c经过点A、B、C,
则$\left\{\begin{array}{l}a+b+c=0\\ 9a+3b+c=0\\ c=3\end{array}\right.$,
解得$\left\{\begin{array}{l}a=1\\ b=-4\\ c=3\end{array}\right.$,
故抛物线的解析式为y=x2-4x+3.
(2)如图1,连接BD.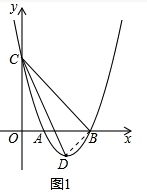
∵y=x2-4x+4-1=(x-2)2-1.
∴D点坐标为(2,-1),
又∵B(3,0),C(0,3),
∴由勾股定理得:CD=$\sqrt{{4}^{2}+{2}^{2}}$=2$\sqrt{5}$,BD=$\sqrt{{1}^{2}+{1}^{2}}$=$\sqrt{2}$,BC=$\sqrt{{3}^{2}+{3}^{2}}$=3$\sqrt{2}$,
在△BCD与△AOC中,$\frac{OA}{BD}$=$\frac{\sqrt{2}}{2}$,$\frac{OC}{BC}$=$\frac{\sqrt{2}}{2}$,$\frac{AC}{CD}$=$\frac{\sqrt{2}}{2}$,
可知,$\frac{OA}{BD}$=$\frac{OC}{BC}$=$\frac{AC}{CD}$,
∴△BCD∽△AOC.
(3)如图2,①过点G作GF⊥x轴,垂足为F.
设点G坐标为(m,m2-4m+3),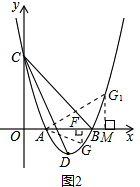
∵CD2=BC2+BD2,
∴△CBD是直角三角形,
∴tan∠GAF=tan∠BCD=$\frac{1}{3}$.
∵tan∠GAF=$\frac{GF}{AF}$=$\frac{1}{3}$,
∴AF=3GF,
即-3(m2-4m+3)=m-1,
解得:m1=1(舍去),m2=$\frac{8}{3}$.
∴点G的坐标为($\frac{8}{3}$,-$\frac{9}{5}$).
②过点G1作G1F⊥x轴,垂足为F.
设点G1坐标为(m,m2-4m+3)
∵CD2=BC2+BD2,
∴△CBD是直角三角形,
∴tan∠G1AF=tan∠BCD=$\frac{1}{3}$.
∵tan∠G1AF=$\frac{GF}{AF}$=$\frac{1}{3}$,
∴AF=3G1F,
即3(m2-4m+3)=m-1,
解得:m1=1(舍去),m2=$\frac{10}{3}$.
∴点G1的坐标为($\frac{10}{3}$,$\frac{7}{9}$).
∵点D的坐标为(2,-1),
∴△ABD是等腰直角三角形,
∴圆心E是线段AB的中点,即E(2,0),半径为1,
设P(x1,y1)(1<x1<3,y1≠0),M(3,y0),作PF⊥x轴,F为垂足.
∵点A、P、M三点在一条直线上,
∴$\frac{\left|{y}_{0}\right|}{\left|{y}_{1}\right|}$=$\frac{2}{{x}_{1}-1}$,即|y0|=$\frac{2\left|{y}_{1}\right|}{{x}_{1}-1}$.
∴tan∠MEB=$\frac{\left|{y}_{0}\right|}{EB}$=$\frac{2\left|{y}_{1}\right|}{{x}_{1}-1}$,
∵AB为直径,
∴∠APB=90°,
∴∠PBA=∠APF,
∴tan∠PBA=tan∠APF=$\frac{{x}_{1}-1}{\left|{y}_{1}\right|}$,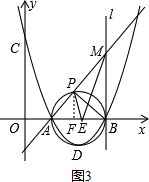
∴tan∠MEB•tan∠PBA=$\frac{2\left|{y}_{1}\right|}{{x}_{1}-1}$•$\frac{{x}_{1}-1}{\left|{y}_{1}\right|}$=2.
另同上,连接PE,
∵PE=1,PF=|y1|,EF=|x1-2|,
在Rt△PEF中,根据勾股定理得:(x1-2)2+y12=1,即1-(x1-2)2=y12,
∵tan∠PBA=$\frac{\left|{y}_{1}\right|}{3-{x}_{1}}$,
∴tan∠MEB•tan∠PBA=$\frac{{2y}_{1}^{2}}{-{x}_{1}^{2}-4{x}_{1}+3}$=$\frac{2{y}_{1}^{2}}{1-({x}_{1}-2)^{2}}$=2.
故答案为2.
点评 本题考查了二次函数综合题,涉及待定系数法求函数解析式、勾股定理、相似三角形的性质、三角形的外接圆、三角函数等知识,综合性强,要求学生有扎实的基本功和探究意识.

| A. | 1.19×1010元 | B. | 11.9×1010元 | C. | 1.19×1011元 | D. | 11.9×1011元 |
| A. | $\frac{x(x-1)}{2}$=930 | B. | $\frac{x(x+1)}{2}$=930 | C. | x(x+1)=930 | D. | x(x-1)=930 |
| A. | 等边三角形 | B. | 平行四边形 | C. | 六边形 | D. | 圆 |
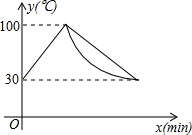 饮水机接通电源就进入自动程序,若在水温为30℃时,接通电源后,水温y(℃)和时间x(min)的关系如图.开机加热时每分钟上升10℃,加热到100℃,饮水机关机停止加热,水温开始下降,下降时水温与开机后的时间成反比例关系.当水温降至30℃,饮水机自动开机,重复上述自动程序.若上午7:20开机,则8:00时能否喝到超过50℃的水?说明理由.
饮水机接通电源就进入自动程序,若在水温为30℃时,接通电源后,水温y(℃)和时间x(min)的关系如图.开机加热时每分钟上升10℃,加热到100℃,饮水机关机停止加热,水温开始下降,下降时水温与开机后的时间成反比例关系.当水温降至30℃,饮水机自动开机,重复上述自动程序.若上午7:20开机,则8:00时能否喝到超过50℃的水?说明理由.