题目内容
14.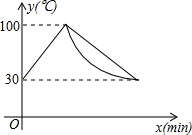 饮水机接通电源就进入自动程序,若在水温为30℃时,接通电源后,水温y(℃)和时间x(min)的关系如图.开机加热时每分钟上升10℃,加热到100℃,饮水机关机停止加热,水温开始下降,下降时水温与开机后的时间成反比例关系.当水温降至30℃,饮水机自动开机,重复上述自动程序.若上午7:20开机,则8:00时能否喝到超过50℃的水?说明理由.
饮水机接通电源就进入自动程序,若在水温为30℃时,接通电源后,水温y(℃)和时间x(min)的关系如图.开机加热时每分钟上升10℃,加热到100℃,饮水机关机停止加热,水温开始下降,下降时水温与开机后的时间成反比例关系.当水温降至30℃,饮水机自动开机,重复上述自动程序.若上午7:20开机,则8:00时能否喝到超过50℃的水?说明理由.
分析 首先根据题意求出两个函数的解析式,然后再求出饮水机完成一个循环周期所需要的时间,再计算求出每一个循环周期内,水温超过50℃的时间段,最后根据时间确定答案.
解答 解:∵开机加热时每分钟上升10℃,
∴从30℃到100℃需要7分钟,
设一次函数关系式为:y=k1x+b,
将(0,30),(7,100)代入y=k1x+b得k1=10,b=30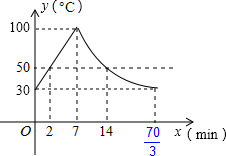
∴y=10x+30(0≤x≤7),令y=50,解得x=2;
设反比例函数关系式为:y=$\frac{k}{x}$,
将(7,100)代入y=$\frac{k}{x}$得k=700,∴y=$\frac{700}{x}$,
将y=30代入y=$\frac{700}{x}$,解得x=$\frac{70}{3}$;
∴y=$\frac{700}{x}$(7≤x≤$\frac{70}{3}$),
令y=50,解得x=14.
所以,饮水机的一个循环周期为$\frac{70}{3}$分钟.每一个循环周期内,在2≤x≤14时间段内,水温超过50℃.
∴7:20开机,则8:00时不能喝到超过50℃的水.
点评 本题主要考查了一次函数及反比例函数的应用题,还有时间的讨论问题.关键是要正确理解题意,计算出饮水机的一个循环周期所用时间.

练习册系列答案
相关题目
2.方程组$\left\{\begin{array}{l}{x+y=5}\\{x-2y=2}\end{array}\right.$的解是( )
| A. | $\left\{\begin{array}{l}{x=1}\\{y=4}\end{array}\right.$ | B. | $\left\{\begin{array}{l}{x=3}\\{y=2}\end{array}\right.$ | C. | $\left\{\begin{array}{l}{x=8}\\{y=-3}\end{array}\right.$ | D. | $\left\{\begin{array}{l}{x=4}\\{y=1}\end{array}\right.$ |
19.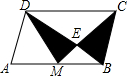 如图,已知M为平行四边形ABCD的边AB的中点,CM交BD于点E,BD=3BE,则图中阴影部分的面积与平行四边形ABCD面积的比是( )
如图,已知M为平行四边形ABCD的边AB的中点,CM交BD于点E,BD=3BE,则图中阴影部分的面积与平行四边形ABCD面积的比是( )
 如图,已知M为平行四边形ABCD的边AB的中点,CM交BD于点E,BD=3BE,则图中阴影部分的面积与平行四边形ABCD面积的比是( )
如图,已知M为平行四边形ABCD的边AB的中点,CM交BD于点E,BD=3BE,则图中阴影部分的面积与平行四边形ABCD面积的比是( )| A. | 1:2 | B. | 2:5 | C. | 3:5 | D. | 1:3 |
3.数据-1、0、$\sqrt{3}$、2.5、2的中位数是( )
| A. | 0 | B. | 2.5 | C. | $\sqrt{3}$ | D. | 2 |
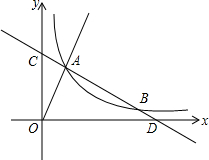 已知直线y=$\frac{1}{2}$x+$\frac{5}{2}$与反比例函数y=$\frac{m}{x}$图象相交于点A、B,OA⊥AB.
已知直线y=$\frac{1}{2}$x+$\frac{5}{2}$与反比例函数y=$\frac{m}{x}$图象相交于点A、B,OA⊥AB. 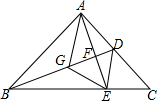 如图所示,已知在△ABC中,BD平分∠ABC交AC于点D,AF⊥BD于点F,延长AF交BC于点E,在BD上取点G,使∠GAF=∠CAF,求证:四边形ACEG是菱形.
如图所示,已知在△ABC中,BD平分∠ABC交AC于点D,AF⊥BD于点F,延长AF交BC于点E,在BD上取点G,使∠GAF=∠CAF,求证:四边形ACEG是菱形.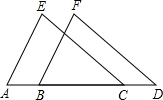 如图,A、B、C、D四点在同一条直线上,AB=CD,EC=DF,EC∥DF.求证:△ACE≌BDF.
如图,A、B、C、D四点在同一条直线上,AB=CD,EC=DF,EC∥DF.求证:△ACE≌BDF.