题目内容
18.(1)计算:$\sqrt{12}$+2-1-|$\sqrt{3}$-2|-3tan60°.(2)先化简,再求值:x•($\frac{1}{x}$-$\frac{1}{x+1}$),其中x=$\sqrt{5}$-1.
分析 (1)直接利用负整数指数幂的性质以及利用二次根式的性质和绝对值的性质和特殊角的三角函数值分别化简求出答案;
(2)直接去括号,利用分式乘法运算法则化简,进而通分化简,再将已知代入求出答案.
解答 解:(1)$\sqrt{12}$+2-1-|$\sqrt{3}$-2|-3tan60°
=2$\sqrt{3}$+$\frac{1}{2}$-(2-$\sqrt{3}$)-3×$\sqrt{3}$
=-$\frac{3}{2}$;
(2)x•($\frac{1}{x}$-$\frac{1}{x+1}$)
=1-$\frac{x}{x+1}$
=$\frac{1}{x+1}$,
把x=$\sqrt{5}$-1代入上式可得:原式=$\frac{1}{\sqrt{5}-1+1}$=$\frac{\sqrt{5}}{5}$.
点评 此题主要考查了实数运算以及分式的化简求值,正确掌握相关性质是解题关键.

练习册系列答案
 口算能手系列答案
口算能手系列答案
相关题目
9.若关于x的不等式组$\left\{\begin{array}{l}{x-a<1}\\{x≥1}\end{array}\right.$的整数解有3个,则a的取值范围是( )
| A. | 3<a≤4 | B. | 2<a≤3 | C. | 2≤a<3 | D. | 3≤a<4 |
7.若多项式m2-2m的值为2,则多项式2m2-4m-1的值为( )
| A. | 1 | B. | 2 | C. | 3 | D. | 4 |
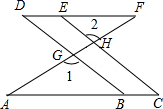 已知:如图,AC∥DF,直线AF分别与直线BD、CE相交于点G,H,∠1=∠2,求证:∠C=∠D.
已知:如图,AC∥DF,直线AF分别与直线BD、CE相交于点G,H,∠1=∠2,求证:∠C=∠D. 如图,在Rt△ABC中,∠BAC=90°,D、E分别是AB、BC的中点,F在CA的延长线上,∠FDA=∠B,AC=6,AB=8,则四边形AEDF的周长为( )
如图,在Rt△ABC中,∠BAC=90°,D、E分别是AB、BC的中点,F在CA的延长线上,∠FDA=∠B,AC=6,AB=8,则四边形AEDF的周长为( ) 证明:三角形中位线定理.
证明:三角形中位线定理. 已知长方形的两条边长分别为4,6.建立适当的坐标系,使它的一个顶点的坐标为(-2,-3).画出示意图,然后写出其他各顶点的坐标.
已知长方形的两条边长分别为4,6.建立适当的坐标系,使它的一个顶点的坐标为(-2,-3).画出示意图,然后写出其他各顶点的坐标.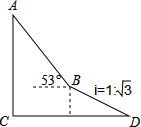 如图,为了测量出楼房AC的高度,从距离楼底C处60$\sqrt{3}$米的点D(点D与楼底C在同一水平面上)出发,沿斜面坡度为i=1:$\sqrt{3}$的斜坡DB前进30米到达点B,在点B处测得楼顶A的仰角为53°,求楼房AC的高度(参考数据:sin53°≈0.8,cos53°≈0.6,tan53°≈$\frac{4}{3}$,计算结果用根号表示,不取近似值).
如图,为了测量出楼房AC的高度,从距离楼底C处60$\sqrt{3}$米的点D(点D与楼底C在同一水平面上)出发,沿斜面坡度为i=1:$\sqrt{3}$的斜坡DB前进30米到达点B,在点B处测得楼顶A的仰角为53°,求楼房AC的高度(参考数据:sin53°≈0.8,cos53°≈0.6,tan53°≈$\frac{4}{3}$,计算结果用根号表示,不取近似值).