题目内容
15．
如图是折幸运星的第一步图解，即将纸带打一个结并拉紧压平，图中AB是这个正五边形的一条边，点C是折叠后的最右边端点，则∠ABC的度数是（ ）| A． | 108° | B． | 120° | C． | 144° | D． | 135° |
分析 先根据正五边形的性质得出正五边形内角的度数，再根据等腰三角形的性质求出∠ABE的度数，进而可得出结论．
解答 解：如图所示：
∵五边形ABCDE是正五边形，
∴其每个内角为108°，且AB=BC=AE，
∴△ABE是等腰三角形，
∴∠ABE=（180°-108°）÷2=36°，
∴∠ABC=180°-36°=144°；
故选：C．
点评 本题考查了图形的折叠问题，熟知折叠是一种对称变换，它属于轴对称，折叠前后图形的形状和大小不变，位置变化，对应边和对应角相等是解答此题的关键．
练习册系列答案
同步练习强化拓展系列答案
相关题目
已知函数y=（m-3）x+n-2（m，n为常数）的图象如图所示，化简：|m-3|-$\sqrt{{n}^{2}-4n+4}$．
证明：三角形中位线定理．
已知长方形的两条边长分别为4，6．建立适当的坐标系，使它的一个顶点的坐标为（-2，-3）．画出示意图，然后写出其他各顶点的坐标．
20．下列判断正确的是（ ）
| A． | “任意选择某一电视频道，它正在播放动画片”是必然事件 | |
| B． | 某运动员投一次篮，投中的概率为0.8，则该运动员投5次篮，一定有4次投中 | |
| C． | 任总抛掷一枚均匀的硬币，反面朝上的概率为$\frac{1}{2}$ | |
| D． | 布袋里有3个白球，1个黑球．任意取出1个球，恰好是黑球的概率是$\frac{1}{3}$ |
7．若多项式m2-2m的值为2，则多项式2m2-4m-1的值为（ ）
| A． | 1 | B． | 2 | C． | 3 | D． | 4 |
4．
如图，CF是△ABC的外角∠ACM的平分线，且CF∥AB，∠ACF=70°，则∠B的度数为（ ）
如图，CF是△ABC的外角∠ACM的平分线，且CF∥AB，∠ACF=70°，则∠B的度数为（ ）| A． | 55° | B． | 60° | C． | 70° | D． | 75° |
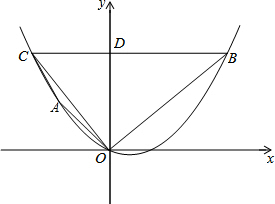如图，在平面直角坐标系xOy中，抛物线y=ax2+bx经过两点A（-1，1），B（2，2）．过点B作BC∥x轴，交抛物线于点C，交y轴于点D．